Preencha cada campo com sua resposta.
Uma partícula percorre o eixo sujeita à ação de uma única força , com em metros e em newtons, conforme mostra a figura .
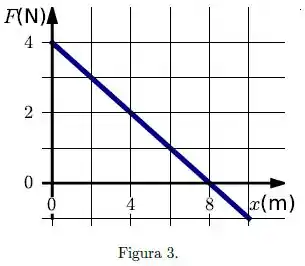
A partícula encontra-se em repouso em . Logo:
- A variação da energia cinética entre e é __.
- A partícula atinge sua velocidade máxima na posição .
Passo 1
Letra a)
A variação da energia cinética é igual ao trabalho realizado entre os dois pontos.
Para achar o trabalho, podemos integrar a equação da força, ou olhar pro gráfico e calcular a área. As áreas abaixo do eixo são trabalhos negativos e acima do eixo trabalhos positivos.
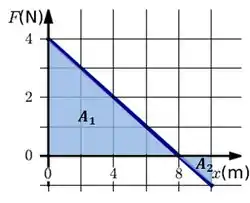
Por integral, teríamos:
A variação da energia cinética entre e é
Passo 2
Letra b)
Agora vamos interpretar o gráfico.
Quando a força é positiva, ela está cedendo energia à partícula e acelerando ela (que estava em repouso no início).
Quando a força passa a ser negativa, a partícula já está se deslocando na direção positiva do eixo . Isso significa que agora a força está freando a partícula e tirando energia dela.
Assim, a velocidade vai ser máxima no limiar de a força começar a frea-la. No nosso gráfico, isso corresponde a .
Em algum momento, a partícula vai frear completamente, e a força ainda vai ser negativa, o que vai fazer agora a partícula se deslocar no sentido negativo do eixo .
Dessa vez, o raciocínio inverte: Quando a força for positiva, ela começa a frear a partícula.
Novamente, essa mudança de sinal corresponde à velocidade máxima e, pelo gráfico, a .
A partícula atinge sua velocidade máxima na posição .
Resposta
Letra a)
A variação da energia cinética entre e é .
Letra b)
A partícula atinge sua velocidade máxima na posição .