Energia Potencial e Conservação da Energia Mecânica
Uma pequena esfera de massa está pendurada no teto por uma corda de comprimento como indicado na figura. Uma força constante é aplicada à esfera na direção horizontal deslocando-a lentamente desde a posição quando a corda está na vertical até quando a corda faz um ângulo com a vertical. O caminho que a esfera percorre é o arco de círculo . Sabendo que a esfera se encontra em repouso antes e depois do deslocamento, responda em função dos dados do problema. Utilize para a aceleração da gravidade.
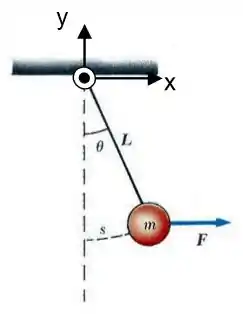
a) Escreva em notação vetorial (em termos dos vetores unitários e ) a tensão na corda para a posição indicada na figura.
b) Desenvolva o teorema trabalho-energia para a situação descrita.
c) Calcule os trabalhos realizados pela tensão, força da gravidade e força . Justifique cada um dos seus cálculos.
d) A origem do potencial está onde a corda está presa no teto. Calcule o valor da energia potencial gravitacional da esfera para posição indicada na figura.
Passo 1
(a)
Para permanecer em equilíbrio: e
Logo, em notação vetorial, isso ficará:
Passo 2
(b)
O teorema trabalho-energia nos diz que o trabalho total é igual a variação da energia cinética.
Como a bola se encontra em repouso antes e depois. Então a variação de energia cinética e nula. Logo teremos:
Passo 3
(c)
A tensão na corda é sempre perpendicular ao deslocamento portanto:
A força da gravidade é conservativa, portanto o trabalho realizado por ela só depende da posição inicial e final. Como ela aponta sempre na direção o seu trabalho é igual a
Sendo a altura final igual a . Temos:
Para calcular o trabalho da força , basta substituir o que já achamos no teorema trabalho-energia:
Passo 4
(d)
Com a origem do potencial no teto, a energia potencial será a mesma, mas negativa:
Resposta
(a)
(b)
(c)
(d)