Passo 1
Para calcular o trabalho realizada em uma volta vamos usar o teorema da enegia cinética. O que ta acontecendo é o seguinte, enquanto o bloquinho da rodando, a força de atrito vai parando ele de pouquinho em pouquinho.
Pra começar, vamos calcular a variação da energia cinética
Sendo assim, vamos usar o teorema da energia cinética
Passo 2
Como já descobrimos o valor do trabalho ao longo de uma curva, vamos usar a fórmula do trabalho para calcular a força de atrito
Onde
Substituindo os valores que já conhecemos na equação do trabalho e isolando o coeficiente de atrito:
Passo 3
Bom, para que a velocidade final seja nula, a energia cinética final tem que ser
Isolando o ficamos com
Resposta
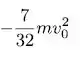
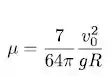
Exercícios de Livros Relacionados
Um caixote de 230k g está pendurado na extremidade de uma corda de comprimento L = 12,0m . Você empurra o caixote horizontalmente com uma força variável F → , deslocando-o para o lado de uma distância
Se um carro com uma massa de 1200k g viaja a 120k m / h em uma rodovia, qual é a energia cinética do carro medida por alguém que está parado no acostamento?
A Fig. 7-26 mostra uma vista superior de três forças horizontais atuando sobre uma caixa que estava inicialmente em repouso e passou a se mover sobre um piso sem atrito. Os módulos das forças são F 1=
Uma mola e um bloco são montados como na Fig. 7-9. Quando o bloco é puxado para o ponto x=+ 4,0c m , devemos aplicar uma força de 360N para mantê-lo nessa posição. Puxamos o bloco para o ponto x=11c m
No arranjo da Fig. 7-9, puxamos gradualmente o bloco de x= 0 até x=+3,0c m , onde fica em repouso. A Fig. 7-34 mostra o trabalho que nossa força realiza sobre o bloco. A escala vertical do gráfico é d