USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 55
Uma partícula de massa desloca-se ao longo de uma reta. Entre e , ela está sujeita à uma força representada no gráfico da figura . Calcule a velocidade da partícula depois de percorrer e , sabendo que sua velocidade para é de .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma partícula de massa que tá percorrendo uma distância de a e sujeita a uma força , mostrada no gráfico:
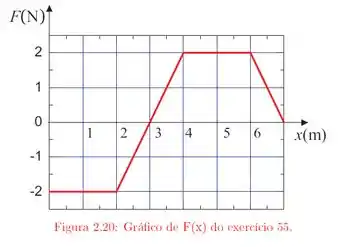
Nós precisamos determinar a velocidade da partícula de a e depois de a . Pra isso, nós temos uma velocidade inicial e precisamos nos lembrar de duas coisas: primeiro, que o valor a área abaixo do gráfico da força versus distância é numericamente igual ao trabalho realizado por essa força; segundo, que pelo teorema do trabalho e energia cinética, temos:
Onde é o trabalho realizado, que é numericamente igual a área abaixo do gráfico, e é a variação de energia cinética do sistema, dada por ( é a velocidade final e é a velocidade inicial). A partir daí, conseguimos encontrar a velocidade da partícula em cada deslocamento considerado.
Vamos lá!
Passo 2
Galera, para determinar a velocidade da partícula depois de percorrer , vamos começar encontrando a área abaixo da curva de a . Repare que de a temos um trapézio de “cabeça para baixo”. Repare que a base maior desse trapézio tem , a base menor tem e sua altura é . Assim, a área do trapézio é dada por:
E te até , a gente tem um triângulo de base e altura . Então, sua área vai ser dada por:
Então, a nossa área de a é dada pela área do triângulo menos a área do trapézio (menos, porque o trapézio tá abaixo do eixo ). E como o trabalho é numericamente igual a área, vamos ter:
Assim, pelo teorema do trabalho e energia cinética, temos:
Substituindo , e :
Tirando a raiz dos dois lados, temos nossa velocidade:
Passo 3
Agora, para descobrir a velocidade entre e , vamos fazer algo parecido, observando as figuras geométricas que aparecem abaixo do gráfico e calculando suas áreas para obter o trabalho. A gente já sabe que de a , temos . De a , temos outro trapézio de base , base menor e altura . Assim, a área será:
Assim, usando o teorema do trabalho e energia cinética, temos:
Isolando :
Valeu, galera! Até a próxima! 😉