Um bloco de metal de massa está apoiado numa mesa e está conectado a um bloco de massa através uma corda de massa desprezível. A corda passa por uma polia de massa desprezível, na qual não há atrito. Ao iniciar o movimento, vemos que há atrito cinético sobre a mesa, com coeficiente .
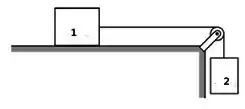
Depois que os blocos se deslocaram de uma distância , podemos dizer que :
- o bloco 1 ganhou energia cinética .
- energia cinética do sistema é que é igual a .
- a energia cinética do bloco 2 é K =
- a energia cinética do sistema é que é igual a
- nenhuma das anteriores.
Passo 1
Utilizando o Teorema Trabalho – Energia para o sistema, teremos:
Como o sistema parte do repouso, teremos:
Logo,
Resposta
Exercícios de Livros Relacionados
Um caixote de 230k g está pendurado na extremidade de uma corda de comprimento L = 12,0m . Você empurra o caixote horizontalmente com uma força variável F → , deslocando-o para o lado de uma distância
Se um carro com uma massa de 1200k g viaja a 120k m / h em uma rodovia, qual é a energia cinética do carro medida por alguém que está parado no acostamento?
A Fig. 7-26 mostra uma vista superior de três forças horizontais atuando sobre uma caixa que estava inicialmente em repouso e passou a se mover sobre um piso sem atrito. Os módulos das forças são F 1=
Uma mola e um bloco são montados como na Fig. 7-9. Quando o bloco é puxado para o ponto x=+ 4,0c m , devemos aplicar uma força de 360N para mantê-lo nessa posição. Puxamos o bloco para o ponto x=11c m
No arranjo da Fig. 7-9, puxamos gradualmente o bloco de x= 0 até x=+3,0c m , onde fica em repouso. A Fig. 7-34 mostra o trabalho que nossa força realiza sobre o bloco. A escala vertical do gráfico é d