Trabalho e Energia Cinética, Energia Potencial e Conservação da Energia Mecânica
Um bloco de massa está acoplado a uma mola de constante elástica sobre uma plataforma horizontal, não havendo atrito entre a plataforma e o bloco. A plataforma se encontra inicialmente sendo sustentada a uma altura em relação ao solo e o bloco estirado de em relação ao ponto de equilíbrio da mola (ver figura).
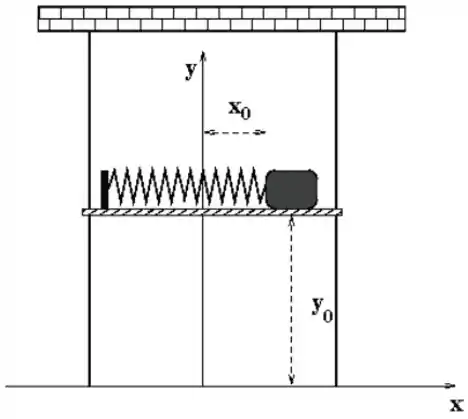
Nesta configuração, simultaneamente a plataforma é solta e começa a cair livremente (escorregando pelas hastes sem atrito) e o bloco é solto.
Sendo assim, havendo saído do repouso, o bloco tem dois movimentos: oscila horizontalmente, enquanto cai em queda livre.
Tome a posição de equilíbrio da mola e a posição no solo (tal como no sistema de referência da figura), e .
a) Calcule o trabalho total sobre o bloco, devido às forças da mola e da gravidade, desde o ponto de partida até atingir uma altura e uma posição horizontal .
b) Justifique claramente porquê as forças envolvidas neste movimento são conservativas.
c) Encontre a velocidade escalar do bloco, , em função de uma altura genérica e posição horizontal . Justifique cuidadosamente os passos para chegar a esta expressão.
d) Observa-se que o bloco tem a mesma velocidade escalar quando está em dois pontos distintos: e . Sabendo que o bloco tem massa , encontre a constante elástica da mola.
Passo 1
a)
O trabalho total é a soma do trabalho realizado pela força da mola e pela força da gravidade.
A força da mola é e a força da gravidade é .
Queremos o trabalho do ponto inicial até o ponto final .
Então o trabalho total é:
Passo 2
b)
O trabalho que obtivemos em (a) só depende dos pontos e , ele não depende da trajetória do bloco entre um ponto e outro. Portanto, as forças envolvidas no movimento são conservativas!
Passo 3
c)
Podemos usar o teorema trabalho-energia cinética, que diz
Vamos aplicar essa fórmula do ponto até um ponto genérico , ok?
Pro trabalho total sobre o bloco vamos pegar a expressão que achamos na letra (a) substituindo o ponto por . Assim,
Além disso, sabemos que o bloco sai do repouso, então .
Passo 4
Show! Então, pelo teorema trabalho-energia cinética, temos
A é a que ele pediu, então vamos chamá-la de mesmo! Então ficou:
Passo 5
d)
Vamos usar a conservação de energia mecânica!
Como todas as forças atuando são conservativas, temos
ou seja a energia mecânica nos pontos são iguais.
E a energia mecânica nada mais é que a soma da energia potencial (gravitacional e elástica) com a energia cinética:
Então temos
Passo 6
Mas o enunciado diz que o bloco tem a mesma velocidade escalar nos 2 pontos, ou seja, . Então a energia cinética é a mesma dos 2 lados e podemos cortá-la!
Então a equação fica
Também sabemos as coordenadas dos pontos: e .
Substituindo os valores:
Como e , isso dá:
Resposta
a)
b)
O trabalho não depende da trajetória do bloco.
c)
d)