Trabalho e Energia
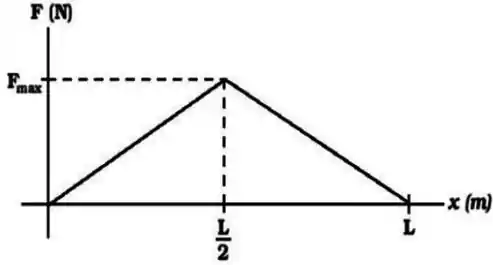
Uma partícula parte do repouso em e desloca-se para , sob a ação de uma força variável mostrada na figura. Qual é a energia cinética das partículas em e em ?
a)
b) ,
c) ,
d) ,
e) ,
Passo 1
Temos um gráfico de Força x Deslocamento, ou seja, a área do gráfico nos dá o trabalho realizado pela partícula. No nosso problema, o trabalho é igual à energia cinética, visto que não foi mencionada qualquer diferença na altura da partícula ou a presença de uma mola.
Logo, basta calcular a área dos dois triângulos:
E também.
Resposta
Alternativa .
Exercícios de Livros Relacionados
Um caixote de 230k g está pendurado na extremidade de uma corda de comprimento L = 12,0m . Você empurra o caixote horizontalmente com uma força variável F → , deslocando-o para o lado de uma distância
Se um carro com uma massa de 1200k g viaja a 120k m / h em uma rodovia, qual é a energia cinética do carro medida por alguém que está parado no acostamento?
A Fig. 7-26 mostra uma vista superior de três forças horizontais atuando sobre uma caixa que estava inicialmente em repouso e passou a se mover sobre um piso sem atrito. Os módulos das forças são F 1=
Uma mola e um bloco são montados como na Fig. 7-9. Quando o bloco é puxado para o ponto x=+ 4,0c m , devemos aplicar uma força de 360N para mantê-lo nessa posição. Puxamos o bloco para o ponto x=11c m
No arranjo da Fig. 7-9, puxamos gradualmente o bloco de x= 0 até x=+3,0c m , onde fica em repouso. A Fig. 7-34 mostra o trabalho que nossa força realiza sobre o bloco. A escala vertical do gráfico é d