Um corpo desliza em um piso horizontal no sentido positivo do eixo enquanto uma força age sobre ele. O corpo parte do repouso na posição e se move até ficar momentaneamente em repouso.
(a) Expresse o trabalho realizado pela força sobre o corpo em função da posição final . Considere como posição inicial .
(b) Esboce o gráfico da forças versus posição. Determine o valor máximo da energia cinética adquirida pelo corpo e em que posição ela ocorre.
(c) Determine, depois de iniciado o movimento, em que posição o corpo fica em repouso momentaneamente?
Passo 1
No letra (a), queremos o trabalho da força até uma posição .
Muitas vezes, calculamos o trabalho de uma força constante .
Quando a força está na mesma direção do deslocamento, temos:
Porém, agora temos uma força variando ao longo do tempo, por isso precisamos calcular o trbalho realizado por cada valor ao longo de um deslocamentozinho que chamamos de infinitesimal ao longo de .
A soma desses trabalhos ao longo de todo o deslocamento será dado pela integral dessa expressão:
Além disso, a posição vai variar de até uma posição . Então, nossos lmites da integral ficam:
Integrando isso, temos:
Aplicando nos intervalos:
Agora, temos o valor do trabalho para um deslocamento até uma posição qualquer .
Passo 2
Na letra (b), queremos o gráfico e o valor de energia cinética máxima.
Vamos começar desenhando esse gráfico.
O gráfico da força ao longo de será uma reta decrescente começando em quando e com raiz em :
O gráfico fica assim.
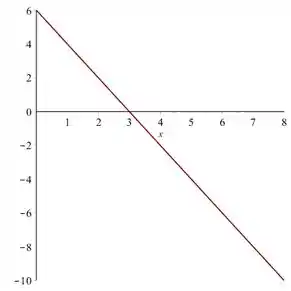
Se a força está na direção do eixo , temos que a partir de a força atua no sentido contrário do deslocamento.
Passo 3
Queremos o energia cinética máxima .
Pelo teorema trabalho-energia cinética:
Como a energia cinética inicial é nula (repouso), temos que o trabalho da força será igual à energia cinética final:
Mas em que posição temos a velocidade do corpo máxima ?
Olhando novamente para o gráfico da força:
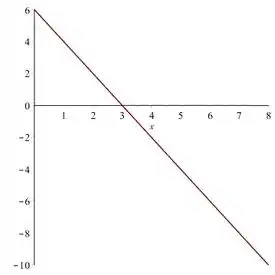
No intervalo de a a força é positiva e faz o corpo ganhar velocidade.
Porém, após a posição , a força é negativa e passa a atuar contra o deslocamento do corpo, assim sua velocidade passa a diminuir.
Então o ponto de valocidade máxima será em .
Passo 4
A energia cinética máxima, será:
Podemos substistuir na expressão do trabalho:
Ou então podemos calcular a partir da área abaixo da reta no gráfico, isso porque a integral tem o valor da área abaixo da curva de um gráfico.
Então, aquele triângulo tem área:
Passo 5
Na letra (c), queremos a posição na qual a velocidade volta a ser zero.
Lembra que vimos que a partir de a força atua contra o movimento, diminuindo a velocidade do corpo?
Então, em algum momento esse corpo vai parar novamente.
Para descobrirmos essa posição podemos simplesmente achar quando nossa energia cinética volta a ser nula:
Já achamos que a expressão para a energia cinética será igual ao trabalho realizado por :
Então, com essa expressão, estamos achando em qual posição a energia cinética vale zero.
Colocando em evidência, temos:
A primeira raiz será:
Enquanto a segunda raiz será:
Então, na posição , a energia cinética do corpo volta a ser nula e ele para momentaneamente.
Resposta
(a)
(b)
(c)