Na figura abaixo, um bloco de massa desliza ao longo de uma pista, de um nível para outro mais elevado, passando por um vale intermediário. A pista não possui atrito até o bloco atingir o nível mais alto, onde uma força de atrito faz o bloco parar ao percorrer uma distância . A velocidade do bloco no ponto é , a diferença de altura é e coeficiente de atrito cinético é . Considere .
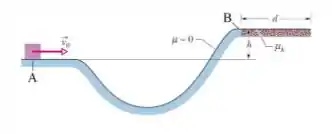
Determine:
(a) A variação da energia potencial gravitacional quando o bloco se desloca de para .
(b) O módulo da velocidade inicial .
(c) A distância .
Passo 1
a) Tomando como nível de referência ( e ) a altura do bloco na posição A. Assim, a variação da energia potencial gravitacional quando o bloco se desloca de A para B é de:
Passo 2
b) Conservando a energia mecânica entre os pontos A e B temos:
Passo 3
c) Usando o teorema do trabalho-energia cinética durante o deslocamento temos que:
Onde . Logo:
Resposta
a)
b)
c)