Trabalho e Energia Cinética, Forças e Leis de Newton
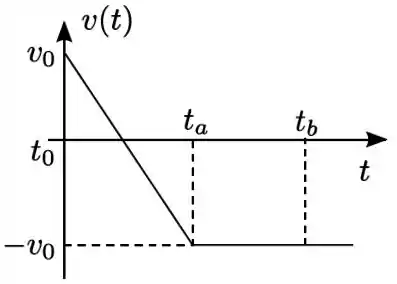
Uma partícula desloca-se em um determinado trajeto e sua velocidade em função do tempo é descrita de acordo com o gráfico apresentado na figura. Considere os instantes , e . Os trabalhos realizados pela força resultante sobre a partícula entre e , , e entre e , , são dados por
(a) e
(b) e
(c) e
(d) e
(e) e
Passo 1
Vamos começar focando no trajeto da partícula entre o tempo e o tempo .
Pelo teorema trabalho-energia cinética, o trabalho realizado pela força resultante (no caso ) é igual à diferença de energia cinética :
Passo 2
Vamos considerar que a partícula tem massa , beleza?
Olhando o gráfico, podemos ver que a velocidade vale em , portanto a energia cinética inicial é
Depois, a velocidade da partícula vai descendo, de maneira constante, até valer em . Ou seja, a energia cinética final é
Passo 3
Então temos
Passo 4
Agora vamos ver o trajeto entre os tempos e .
Nesse trajeto, a velocidade do bloco é constante em : o bloco está numa MRU. Portanto, sua aceleração é nula. Então pela 2ª lei de Newton, a força resultante agindo sobre ele também é nula!
E se não tem força agindo, não tem trabalho!
Ou seja,
Resposta
Alternativa (a)