Um bloco de massa m=3,0 Kg, partindo do repouso, é puxado sobre uma superfície horizontal sem atrito por uma força F cuja direção é sempre constante e horizontal. O módulo da força é variável, conforme o gráfico ao lado.
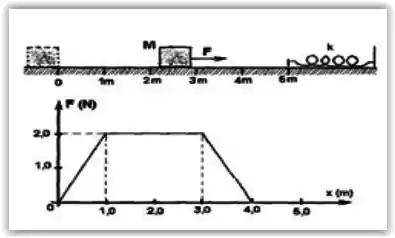
(a) Determine o trabalho realizado pela força desde x = 0 até 5,0 m.
(b) Calcule a velocidade do bloco quando ele atinge a posição x = 5,0 m.
(c) Após percorrer toda a superfície mostrada na figura o bloco é freado por uma mola de constante elástica k = 300 N/m. Determine a compressão máxima da mola.
Passo 1
O item (a) pede o trabalho realizado pela força desde x=0 até 5,0 m.
Sabemos que quando temos o gráfico da força pelo deslocamento, podemos achar tranquilamente o valor do trabalho pela área desse gráfico:
Assim temos que área do gráfico:
Passo 2
O item (b) nos pede a velocidade do bloco quando ele atinge a posição x=5.
Temos pelo teorema do trabalho-energia cinética a seguinte fórmula:
Podemos, a partir dessa fórmula, obter a energia cinética final. Então, montamos:
Como o bloco parte do repouso em x=0, sua velocidade inicial é nula e, portanto, sua energia cinética também. Assim montamos:
Temos o valor do trabalho, calculado no passo anterior, e o valor da massa do bloco é 3,0 kg.
Substituindo, chegamos a:
Passo 3
O item (c) quer saber qual será a compressão da mola, após o bloco percorrer toda a superfície.
Como durante a compressão da mola a única força que age sobre o bloco é a força elástica, a energia mecânica do bloco se conserva.
Então, iremos aplicar a conservação da energia mecânica.
Inicialmente, quando o bloco toca na mola ele tem apenas energia cinética. No momento em que sua compressão máxima é alcançada, ele tem somente energia potencial elástica. Sendo assim, podemos montar:
Como no momento em que o bloco toca na mola ele tem velocidade de 2m/s e sua massa é de 3 kg, temos:
Igualando os dois: