Um bloco de está em repouso sobre uma superfície horizontal e preso a uma mola de constante elástica . O bloco é arrastado, distendendo a mola de , pela força como mostra a figura. A força de atrito da superfície sobre o bloco é de . Dado que , e , a velocidade do bloco no final deste deslocamento é

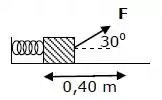
(A)

(B)

(C)

(D)

(E)

Quem são essas forças?

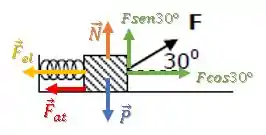
Então, o teorema fica assim:

Eita... tem um monte de forças ai, né.

Mas relaxa, é mais simples do que parece.

Um detalhe importantíssimo é que apenas forças na mesma direção do deslocamento realizam trabalho. Sendo que as forças “inclinadas” tem uma componente na direção do deslocamento que realiza trabalho e uma componente perpendicular ao deslocamento que não realiza trabalho (como é o caso de ).

É daí que vem aquela história do trabalho ser o produto escalar entre a força e o deslocamento:

Então:

Opa, já melhorou um pouquinho:

Agora, basta calcular esses trabalhos e jogar na expressão.

A força de atrito é contrária ao deslocamento, portanto seu trabalho será negativo:

O trabalho da força elástica também é negativo, pois a força também é contra o deslocamento:

Enquanto o trabalho da componente de na direção do deslocamento é:

Logo:

Como o bloco parte do repouso, sua velocidade inicial é nula:

Assim, achamos que a velocidade final do bloco é aproximadamente:

Ficamos com a letra (A).