Um bloco de massa está pendurado, através de um fio leve que passa por uma polia sem massa e sem atrito, a um segundo bloco, também de massa . O coeficiente de atrito cinético entre o bloco e a mesa é 0,40. O bloco sobre a mesa é empurrado contra a mola, comprimindo-a de a partir de sua posição relaxada. A mola tem uma constante elástica de .
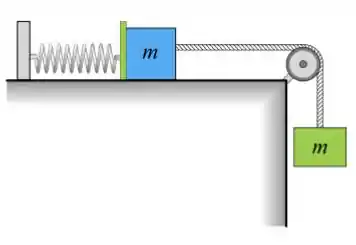
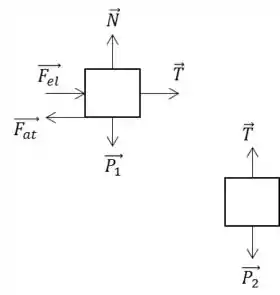
a) Mostre o diagrama das forças que atuam em ambos os blocos imediatamente após o bloco sobre a mesa ser solto.
b) Calcule o trabalho da força de atrito no bloco sobre a mesa até que a mola volte à sua posição relaxada
c) Calcule o trabalho da força peso do bloco pendurado enquanto a mola volta à sua posição relaxada;
d) Calcule a velocidade dos dois blocos no instante em que o bloco pendurado desceu .
Passo 1
a)
O diagrama de blocos vai ficar:
Passo 2
b)
Utilizando a fórmula do trabalho temos:
Utilizando a fórmula da força de atrito:
Como o bloco está em equilíbrio da vertical, sabemos que .
Agora é só substituir os dados, não se esqueça de passar a distancia percorrida para metros, .
Passo 3
c)
Como os blocos estão ligados por um fio, temos que o bloco pendurado vai descer uma altura .
Passo 4
d)
Aplicando o teorema trabalho-energia:
Resposta
a)
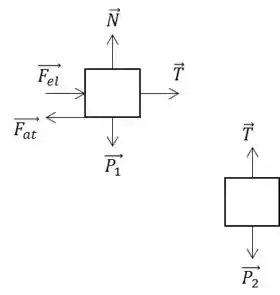
b)
c)
d)