[Enunciado comum às Questões 3 e 4]
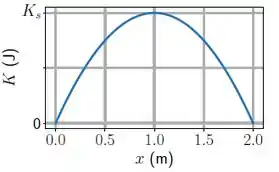
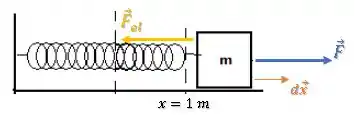
Um bloco de massa repousa em uma superfície horizontal sem atrito e está preso a uma mola de constante elástica e massa desprezível. A extremidade oposta da mola é mantida presa a uma parede. O bloco está em repouso na posição em que a mola está relaxada (). Nesta situação uma força constante ́é aplicada no sentido positivo do eixo . A figura mostra o gráfico da energia cinética do bloco em função da posição após a aplicação da força. Considere .
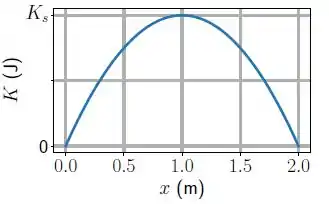
[Questão 3]
Julgue as assertivas abaixo, considerando que o bloco move-se na direção do eixo positivo:
. A variação de energia cinética é igual ao trabalho da força .
. O trabalho da força elástica é negativo.
. A energia mecânica total do sistema é .
É correto apenas o que se afirma em:
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Passo 1
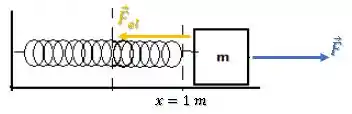
A situação é a seguinte, temos um bloco preso a uma mola na posição , com a mola relaxada:
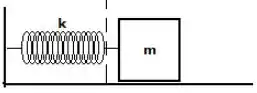
Em um dado instante, uma força passa a puxar o bloco:
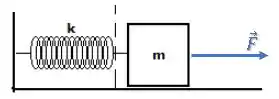
Nesse primeiro instante, a força resultante será a própria força , gerando uma aceleração para a direita no bloco e fazendo ele ganhar velocidade. Assim, sua energia cinética vai aumentar.
Porém, quando o bloco vai esticando a mola, ela vai exercer uma força elástica no sentido contrário:
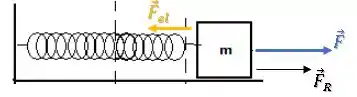
Mas a força resultante ainda estará no sentido positivo do eixo e o bloco continua acelerando e ganhando energia cinética.
Isso vai acontecer até o momento em que a força elástica chega no mesmo valor de , quando isso acontecer, a força resultante sobre o bloco será nula e ele vai parar de ganhar energia cinética
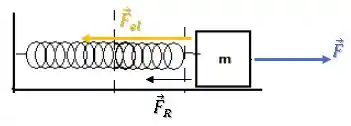
Depois disso, a força elástica fica ainda maior, gerando uma força resultante assim como uma aceleração no sentido contrário, fazendo o bloco diminuir sua velocidade e perder energia cinética até finalmente parar:
Tendeu agora aquele gráfico lá da energia cinética??
Então, vamos para as afirmativas.
Passo 2
. A variação de energia cinética é igual ao trabalho da força .
Existe aquele teorema que relaciona o trabalho e energia cinética ,né?
O famoso Teorema Trabalho-Energia Cinética:
Então, parece que a afirmativa está correta, né?
NÃOOOO, muito cuidado.
O teorema diz que o trabalho RESULTANTE é igual à variação de energia cinética.
Ao longo do deslocamento do bloquinho, existem duas forças atuando sobre ele, a força e a força elástica :
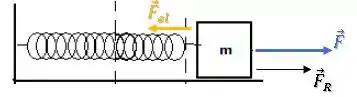
Então, aplicando o teorema aqui, teríamos que o trabalho resultante seria a soma dos trabalhos dessas duas forças:
Assim, a nossa afirmativa está na verdade errada.
A afirmativa é falsa.
Passo 3
. O trabalho da força elástica é negativo.
A força elástica está atuando contra o deslocamento, né?
Então seu trabalho será realmente negativo... dá uma olhada aqui no porque.
O trabalho da força elástica é dado pelo produto vetorial entre e o vetor deslocamento :
O módulo de na verdade vai variar, porém vamos nos concentrar no sinal...
Vimos que ao longo de todo o deslocamento, a força elástica estava contrária ao deslocamento (em laranja):
Assim, temos que o ângulo entre esses vetores é :
Ou seja, o trabalho da força elástica realmente será negativo.
A afirmativa é verdadeira.
Passo 4
. A energia mecânica total do sistema é .
Isso não está correto, porque a força não é uma força conservativa e está realizando trabalho sobre o bloco, o que faz a energia mecânica variar.
Se a energia mecânica varia, ela não vai ser sempre igual a .
Só para pegar um contra-exemplo aqui, podemos pegar o ponto do gráfico de energia cinética:
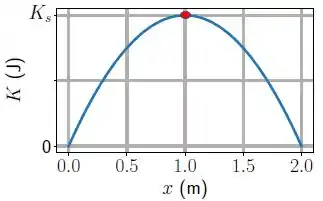
A energia mecânica vai ser a soma da energia potencial elástica com a energia cinética :
Como a constante elástica é positiva, temos que a energia mecânica certamente é maior que .
A afirmativa é falsa.
Como apenas a afirmativa está correta, ficamos com a letra (b).
Resposta
Letra (b)