Um bloco de massa é solto do repouso de uma altura desconhecida acima de uma mola relaxada posicionada na vertical e com constante elástica. O bloco gruda na mola e a comprime de até parar momentaneamente. Despreze atritos.
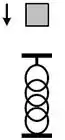
a) Calcule o trabalho realizado pela força da gravidade sobre o bloco durante a compressão da mola.
b) Calcule o trabalho realizado pela mola sobre o bloco durante a sua compressão.
c) Calcule o módulo da velocidade do bloco imediatamente antes dele colidir com a mola.
Passo 1
Vamos entender o que significam algumas palavras desse enunciado:
Um bloco de massa é solto do repouso (, de uma altura desconhecida acima de uma mola relaxada (a energia potencial elástica inicial é zero) posicionada na vertical e com constante elástica. O bloco gruda na mola e a comprime de (cm não é unidade do SI, então passa pra metro: ) até parar () momentaneamente. Despreze atritos.
Beleza, já temos bastante informação. Vamos ver o que ele tá pedindo.
Passo 2
a)A gente quer o trabalho realizado pela força da gravidade sobre o bloco durante a compressão da mola.
Essa tal força da gravidade nada mais é do que o peso!
Então vamos calcular o trabalho do peso ao comprimir a mola em .
Onde esse é o ângulo entre a força peso e o deslocamento y:
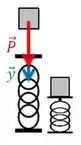
O ângulo entre eles é zero, olha ali na figura:
E
Então:
Sucesso??
Passo 3
b)
Agora ele quer saber o trabalho realizado pela mola. Pra isso, a gente vai usar o teorma Trabalho x Energia Potencial.
O que ele fala pra gente é: A força elástica é uma daquelas forças conservativas, assim como o peso, isso quer dizer que a gente calcula o trabalho dela como sendo menos a variação da energia potencial, assim:
Lembra lá no passo 1 que a gente destacou a informação de que, na situação inicial, a mola estava relaxada, e que por isso ela não tem energia armazenada. Então, vamos usar isso agora:
Passo 4
c)
Ele ta pedindo a velocidade do bloco imediatamente antes dele atingir a mola.
Como que a gente pode resolver isso? Podemos tentar conservação da energia mecânica entre o ponto em que o bloquinho ta na altura mais alta e o ponto em que ele já comprimiu a mola em 10cm? Huum... Vamos ver:
A energia mecânica inicial seria:
Olha lá no passo 1. A gente não sabe a altura em que o bloquinho começa, então não podemos usar conservação da energia mecância aqui!
Tá, mas e agora???
Passo 5
Eis que surge o teorema Trabalho x Energia Cinética!!
A gente calculou, nas letras a e b, os trabalhos gravitacional (força peso) e o da mola (força elástica).
Usando o teorema trabalho x energia cinética:
(Lá no passo 1 a gente viu que a velocidade final, quando o bloquinho já comprimiu a mola de 10cm, era 0). Aí é só ajeitar e fazer as continhas:
Resposta
a)
b)
c)