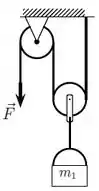
Um fio ideal tem uma de suas extremidades presa no teto e passa por duas polias também ideais. Uma lata com uma massa está pendurada em uma das polias (por um fio também ideal) e uma força de módulo desconhecido é aplicada por uma pessoa na extremidade livre do fio de maneira que a lata sobe com velocidade constante. A situação está representada na figura ao lado.
(b) Qual o trabalho realizado por cada uma das forças que atuam sobre a lata quando a
mesma sobe uma distância conhecida?
Passo 1
b) Calcularemos o trabalho de cada uma das forças que atuam sobre a lata:
Sabendo que apenas a força peso e a tração atuam sobre a lata, teremos:
Trabalho da força peso (negativo, pois é contrário ao movimento do corpo):
Trabalho da força de tração:
De acordo com o teorema Trabalho e Energia Cinética:
“O somatório dos trabalhos é igual à variação da energia cinética”.
Como a lata sobe com velocidade constante, não há variação da energia cinética. Assim: