Halliday - Vol.1 - Ed. 8 - Capítulo 7 – Seção 5 – Questão 13
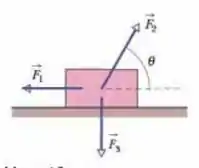
(Capítulo 7.5 – Exercício 13) A Fig. 7-27 mostra três forças aplicadas a um baú que se desloca para a esquerda sobre um piso sem atrito. Os módulos das forças são , e ; o ângulo indicado é . No deslocamento, (a) qual é o trabalho total realizado sobre o baú pelas três forças e (b) a energia cinética do baú aumenta ou diminui?
Passo 1
E aí galerinha, vamos pra mais um exercício sobre energia cinética e trabalho?
Aqui temos um baú que anda pra esquerda a partir de 3 forças aplicadas nele
O que a gente quer saber é a) qual o trabalho que o baú realiza com essas 3 forças e b) se a energia cinética ta aumentando ou diminuindo
Como as forças são constantes, o trabalho realizado por elas é dado por , em que é o deslocamento.
Então, pro primeiro item vamos usar:
Para cada força invididualmente, em que é o ângulo do deslocamento. Aí depois é só somar os trabalhos das 3 forças para termos o trabalho total
Pra sabermos se a energia cinética está crescendo ou diminuindo, vamos lembrar que
Bora?
Passo 2
a) Como a força age na direção do deslocamento, temos que:
Como a força faz um ângulo de com a direção do deslocamento, temos que:
Como a força é perpendicular à direção do deslocamento,
Pois .
Dessa forma, trabalho total realizado pelas três forças é:
Passo 3
b) Bom pessoal, nós sabemos que:
Logo,
Ou seja, a energia cinética aumenta de 1,50 J durante o deslocamento .
De boa pessoal??? Bora resolver mais questões então!!!!!
Resposta
a)
b) – a energia cinética aumenta