Trabalho e Energia Cinética
1a) Na figura, um bloco de tem velocidade inicial em um instante quando se choca com uma mola relaxada . O bloco comprime a mola até um valor máximo e depois a mola empurra de volta o bloco até o ponto inicial. Neste instante, , a velocidade final é . Durante todo percurso existe atrito cinético. Calcule o trabalho da gravidade , o trabalho da mola e o trabalho do atrito entre os instantes e .
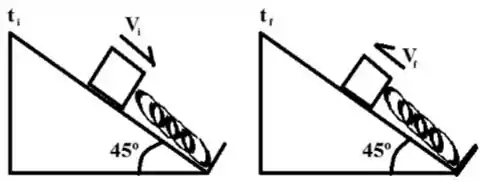
Passo 1
Pelo teorema trabalho-energia temos:
Neste caso:
Como a força da gravidade e a força elástica da mola são forças conservativas, e como nos instantes e o bloco se encontra na mesma posição, então , não teve variação nem de altura nem da posição da mola. Logo:
Assim:
Substituindo os dados:
Resposta
Exercícios de Livros Relacionados
Um caixote de 230k g está pendurado na extremidade de uma corda de comprimento L = 12,0m . Você empurra o caixote horizontalmente com uma força variável F → , deslocando-o para o lado de uma distância
Se um carro com uma massa de 1200k g viaja a 120k m / h em uma rodovia, qual é a energia cinética do carro medida por alguém que está parado no acostamento?
A Fig. 7-26 mostra uma vista superior de três forças horizontais atuando sobre uma caixa que estava inicialmente em repouso e passou a se mover sobre um piso sem atrito. Os módulos das forças são F 1=
Uma mola e um bloco são montados como na Fig. 7-9. Quando o bloco é puxado para o ponto x=+ 4,0c m , devemos aplicar uma força de 360N para mantê-lo nessa posição. Puxamos o bloco para o ponto x=11c m
No arranjo da Fig. 7-9, puxamos gradualmente o bloco de x= 0 até x=+3,0c m , onde fica em repouso. A Fig. 7-34 mostra o trabalho que nossa força realiza sobre o bloco. A escala vertical do gráfico é d