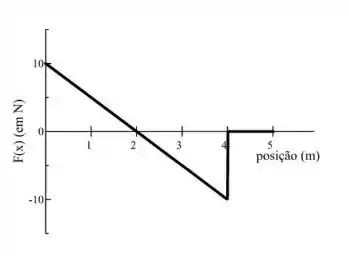
Uma partícula de 4,0 kg, com velocidade inicial igual a 2m/s na posição x = 0m, acelera ao longo do eixo x sujeita a uma força variável representada pelo gráfico mostrado na figura. Sobre a velocidade instantânea da partícula, é CORRETO afirmar que:

Marque a afirmação CORRETA a respeito do trabalho total realizado após as repetições

a) é -2m/s na posição x = 4m

b) é nula na posição x = 2m

c) é nula na posição x = 5m

d) é 3m/s na posição x = 2m

e) é √5 m/s na posição x = 2m

Mais uma questãozinha de trabalho! Como a gente já sabe, o trabalho é:

Mas também sabemos que o trabalho também pode ser calculado como o produto da Força vezes o deslocamento! e dá uma olhada no nosso gráfico! É um grafico de Força por Deslocamento, então a área do nosso gráfico vai dar o trabalho, e como temos a velocidade inicial (2m/s) podemos descobrir a velocidade final de qualquer ponto no gráfico! Quer ver? Bora lá!

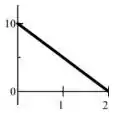
Caculando a área desse triângulo, temos:

Então... W=10J, logo:

Sacou? Então vamo continuar... OPS! Esse resultado já tá na letra d)!

Então já fechamos a questão! :D Showwwwww