Uma bola de massa é lançada do solo com uma velocidade inicial de módulo em uma direção que faz um ângulo com a horizontal. Durante todo seu movimento ela está sob a ação da força peso e da força de resistência do ar. Observa-se que a bola atinge o ponto de altura máxima , com velocidade de módulo . Qual o trabalho realizado pela força de resistência do ar entre o lançamento da bola e o instante em que ela atinge a altura máxima?
Passo 1
Temos uma bola em um lançamento oblíquo com uma velocidade :
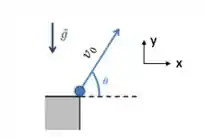
Quando a bola atingir a altura máxima (), ela vai ter sua velocidade igual a .
Já estamos acostumados que a força peso faz a bola perder velocidade na subida, ou seja, temos energia cinética sendo transformada em energia potencial gravitacional.
Porém, agora temos uma força de resistência do ar que também faz a bola perder velocidade. Ela funciona como uma força de atrito, retirando energia do sistema.
O problema quer que a gente ache o trabalho dessa força de resistência do ar () até o instante que a bola chega em .
Passo 2
Precisamos achar o trabalho de uma força. O problema deu para a gente tanto a velocidade inicial () quanto a velocidade final () da bola. Com isso a gente consegue calcular a energia cinética inicial e final.
Isso tudo permite a gente aplicar o teorema trabalho-energia cinética:
Passo 3
Quem vai ser o trabalho total das forças externas?
Vai ser a soma do trabalho da força peso com o trabalho da força de resistência do ar:
Mas o trabalho da força peso, nós sabemos calcular já que temos a diferença de altura. Além disso, ele será negativo já que a bola sobe a a força peso aponta para baixo:
Substituindo os dados de massa da bola () e da diferença de altura ():
Então, temos que o trabalho total () é:
Passo 4
Vamos calcular a variação de energia cinética.
A energia cinética é calculada por:
Então:
Passo 5
Agora, podemos substituir o que achamos para () e () e encontrar o trabalho da resistência do ar ():
Substituindo o valor dado de :