UFRJ – Física 1 – P2 – 2019.2 – Questão 1
Uma força paralela ao eixo é aplicada a um trenó de massa que se desloca sobre uma superfície lisa (sem atrito). A força tem direção e sentido de e seu componente varia com a coordenada do modo indicado no gráfico.
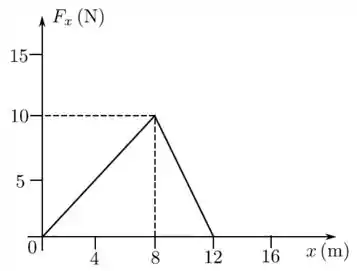
A opção CORRETA é
- A variação de energia cinética é nula entre e
- O trabalho da força é positivo entre e e negativo entre e
- A variação de energia cinética é igual a , entre m e
- A variação de energia potencial é igual a , entre e
- A variação de energia mecânica é igual a , entre x = 0 m e x = 12 m
Passo 1
Se liga! Vamos verificar as alternativas dadas.
Na alternativa (a), ele diz que a variação da energia cinética entre o intervalo m e é nula. Para saber se é verdade, precisamos lembrar o teorema Trabalho-Energia Cinética. Onde temos que
Para saber o trabalho através do gráfico só precisamos calcular a área sob a curva. Repara que é um triângulo de base 12 e altura 10.
Portanto
A alternativa (a) está errada.
Passo 2
A alternativa (b) está errada, pois como toda a curva está acima da parte positiva do eixo , temos que o deslocamento e a força são positivos, logo todo o trabalho é positivo.
Passo 3
Já calculamos a variação da energia cinética na alternativa (a). Lembra que encontramos que
Portanto a alternativa (c) é a correta.