UFABC – Fenômenos Mecânicos – Lista 4 – Questão 03
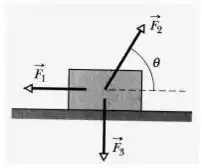
A figura mostra três forças aplicadas a um baú que se desloca para a esquerda sobre um piso sem atrito. Os módulos das forças são , e ; o ângulo indicado é . No deslocamento,
(a) qual é o trabalho total realizado sobre o baú pelas três forças e
(b) a energia cinética do baú aumenta ou diminui?
Passo 1
Oi pessoal, tudo bem? Vamos começar? Temos um bloco sobre uma superfície lisa e nesse bloco agem 3 forças. No entanto o deslocasmento do bloco é para a esquerda (na horizontal) então apenas as componentes horizontais das forças (quando houver) é que serão responsáveis pelo trabalho realizado!
Sendo assim, para calcular o trabalho vamos usar sua descrição pelo produto escalar!
Então galera , como as forças são constantes, o trabalho realizado por elas é dado por
em que é o deslocamento.
E na letra (b), depois com o trabalho calculado, vamos lembrar do teorema trabalho energia!
Vamos lá?
Passo 2
Letra (a):
Como a força age na direção do deslocamento (para esquerda na horizontal, assim ), temos que :
Tranquilo?
Agora vamos analisar as outras forças!
Passo 3
Agora a força !
Como a força faz um ângulo de com a direção do deslocamento, temos que o trabalho realizado por ela é:
Beleza?
Passo 4
Já a força é perpendicular à direção do deslocamento ,
Pois .
Notem que quando a força não tem componente ao longo do deslocamento, essa força não faz parte do deslocamento (seja ajudando, como a força , ou atrasando, como o atrito – que aqui não existe)
Certo? Agora é só somar os trabalhos!
Passo 5
Dessa forma , trabalho total realizado pelas três forças é :
Passo 6
Letra (b): lembrando do teorema trabalho-energia: o trabalho realizado pela força resultante (ou equivalentemente o trabalho total do corpo) é igual a variação de energia cinética
Aí:
Logo ,
Ou seja , a energia cinética aumenta de 1,50 J durante o deslocamento .
E é isso! Espero ter ajudado!