USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte I -Cinemática, Leis de Newton, Trabalho e Energia, Questão 54b
Uma partícula move-se. sob a ação da força , no plano . Calcule:
O trabalho realizado pela força ao longo da diagonal do quadrado da trajetória da figura , partindo da posição e chegando a posição .
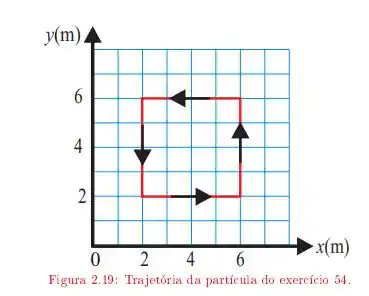
Passo 1
Eaew, tudo certinho?
Temos uma partícula se movendo sobre a ação da força
no plano pela trajetória
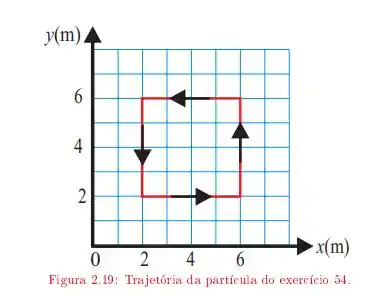
Na alternativa anterior obtivemos que o trabalho realizado ao longo da trajetória completa foi
indicando que esta força não é conservativa, já que o trabalho sobre uma trajetória fechada foi diferente de zero. Sendo assim, para encontrarmos a alternativa
O trabalho realizado pela força ao longo da diagonal do quadrado da trajetória da figura , partindo da posição e chegando a posição .
Iremos precisar usar a definição de trabalho como
Bora lá!
Passo 2
Usando que
o produto escalar no integrando de nosso trabalho é tal que
Ou seja, temos que resolver
Não é trivial escolher os limites de integração nesta situação! Portanto, para facilitar o problema vamos tentar deixar tudo em termos de uma única variável ou , como fazemos isso?
Passo 3
Vamos tentar encontrar a equação da reta que liga o ponto e o ponto . A equação de uma reta é da seguinte maneira
como temos pontos da forma e , obtemos duas equações para os parâmetros
e, da mesma forma
usando dentro de podemos obter
de forma que . E, voltando em qualquer uma das equações acima podemos obter que
e, sendo assim, a equação da reta é
Vamos usar isso para resolver a nossa integração!
Passo 4
Substituindo o resultado em nosso integrando temos que
note que . Aí está! Te vejo na próxima! Tchau Tchau!