Um pêndulo simples consiste numa massa presa a uma corda de comprimento e de massa desprezível. A massa é solta quando a corda faz um ângulo de com a vertical. Considere os trabalhos realizados pela força peso e pela tensão na corda desde a liberação da massa até o instante em que ela passa pelo ponto mais baixo. Os trabalhos realizados pelo peso () e pela tensão () são, respectivamente
(a) ,
(b) ,
(c) ,
(d) ,
(e) ,
Passo 1
Vamos olhar dois momentos as forças sobre a nossa massa
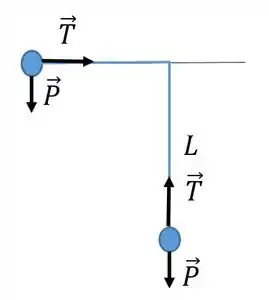
O trabalho do peso pode ser relacionado com a variação da energia potencial gravitacional
A variação é por que o corpo desceu.
Passo 2
Durante todo o trajeto a tensão é sempre perpendicular ao deslocamento da massa, assim o trabalho é dado por
Como e são perpendiculares o produto escalar dentro da integral é nulo e então
Resposta
(E)