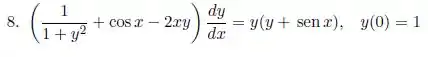
Passo 1
Olhando bem a equação a gente vê que a única forma que sabemos como resolver isso é por equação exata. Vamos manipular essa equação então.
Agora tá com bastante cara de exata e já podemos começar os trabalhos.
Passo 2
Primeiro vamos conferir se ela é realmente exata.
Logo temos realmente uma equação exata. Já podemos aplicar aquele método que já conhecemos bem.
Passo 3
Calculando
Passo 4
Derivando o que obtemos no passo 3 em relação a
Passo 5
Comparando o que obtivemos no passo 4 com
Integrando para encontrar
Passo 6
Vamos ter a nossa solução substituindo o que encontramos no passo 5 com o que encontramos no passo 3
Tomando teremos.
Passo 7
Agora vamos usar a condição inicial, , para encontrarmos o valor de .
Logo a nossa solução será.
Resposta
Exercícios de Livros Relacionados
Em cada um dos problemas 13 e 14, resolva o problema de valor inicial dado e determine, pelo menos aproximadamente, onde a solução é válida 2 x - y + 2 y - x y ' = 0 , y 1 = 3
Verifique se a forma diferencial dada é exata. Justifique. f ) e x 2 + y 2 xd x + yd y
Verifique se a forma diferencial dada é exata. Justifique. i )- y x 2 + y 2d x + x x 2 + y 2 d y ,x , y ∈ Ω , onde Ω é o conjunto x , y ∈ R 2 y0 ∪ { x , y ∈ R 2 | x0 }
Mostre que existem naturais men para os quais a forma diferencial 3 x m + 1 y n + 1 d x + 2 x m + 2 y nd y É exata.
Verifique se a forma diferencial dada é exata. Justifique. d )( x + y )d x + ( x - y ) d y