UFSCAR. Cálculo 3. Lista de Estudos – Integrais Duplas. Questão 3.
3 – Calcular:
Em que é a região delimitada por .
Passo 1
Fala aí! Tudo belezinha por aí? Vamos resolver mais essa questão juntos? Vem comigo!
Bem, o problema pediu pra gente calcular essa integral, que é uma integral dupla
E disse que é pra gente fazer isso na região delimitada por . E como fazemos isso?
Bom, o primeiro passo será entender que região é essa, e para isso nós teremos que desenhá-la. Assim nenhum dado vai passar batido. Então bora fazer isso.
Passo 2
Nossa região de integração foi definida como sendo
E sei que não está tão claro, mas essa é a equação de uma circunferência. Pra gente ver isso melhor vamos reescrever essa equação dessa forma
Podemos somar uma unidade dos dois lados da equação, pois assim ficamos com dois quadrados perfeitos, veja:
Isso porque
E
Então nossa região se torna
E essa é uma circunferência de raio e centro no ponto .
E seu gráfico é dado por:
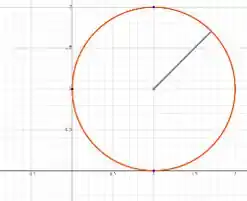
Xiii, temos um problema. Como podemos definir os limites de integração nessa região???
Bom, pra fazer isso nós vamos pensar o seguinte: do jeito que a circunferência está, a gente não consegue integrar, então vamos fazer uma mudança de variáveis para transformar essa região em uma outra circunferência centrada na origem. Isso vai ajudar bastante a gente.
Bora fazer isso no próximo passo.
Passo 3
Vamos fazer uma mudança de variável usando nossa equação da circunferência
Então chamaremos
E
Assim ficamos com:
Que é uma circunferência centrada na origem
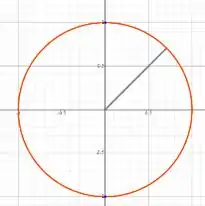
Ahhhh, tem um detalhe bem importante aqui: como estamos fazendo uma mudança de variável, precisamos calcular o Jacobiano dessa transformação. Então precisamos fazer.
Assim,
E
Assim,
E o Jacobiano é dado por:
Com isso, nossa integral que era
Se transforma em
Agora vamos nos concentrar em resolver essa integral.
Passo 4
Podemos passar a integral para coordenadas polares, onde
E as variações de e podem ser vistas no gráfico como:
Transformando a integral em:
Que se transforma em:
Caramba!!! Viu como todas essas manobras ajudaram a melhorar bastante a nossa integral? Parece até tratamento de beleza. Rsrsr
Bora resolver, então.
Passo 5
Usando o Teorema de Fubini, vamos integral de dentro pra fora.
E prontinho. Integral resolvida.