Calcule
Onde é o paralelogramo de vértices , , e .
Sugestão: faça uma mudança de variáveis conveniente.
Passo 1
Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido.
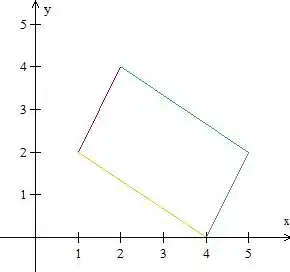
Esse é o paralelogramo da questão. Bom, vamos começar encontrando as equações dessas retas que limitam nossa região. Sabendo que a equação geral da reta , vamos substituir os pontos que definem cada um desses segmentos para encontrar as equações.
Para o segmento vermelho
Substituindo os pontos e , temos:
Temos portanto a equação
Para o segmento verde
Substituindo os pontos e , temos:
Temos portanto a equação
Para o segmento azul
Substituindo os pontos e , temos:
Temos portanto a equação
Para o segmento amarelo
Substituindo os pontos e , temos:
Temos portanto a equação
Passo 2
Ok, e agora? Percebeu que escrever essa região tanto como tipo I ou II vai dar um trabalhinho, não é? Vamos pensar um pouco, repara nas equações das retas que encontramos:
Já deu para ver alguma semelhança aí, né? Vamos reescrever essas equações:
Vamos agora chamar:
Calma, você já vai entender o porquê disso! Aplicando nas equações, temos:
Com essa mudança de variáveis, essas são as equações que passam a limitar nossa região, bem mais bonito, não é? O que nós fizemos, basicamente, foi transformar o nosso paralelogramo do plano em um retângulo bonitinho no plano . Por isso que os intervalos passaram a ser números.
Bom, no plano podemos então descrever a região como
Passo 3
Bom, mas como tudo na vida tem um preço, não poderia ser tão simples assim né.
Temos que calcular o Jacobiano dessa transformação, lembra?
Temos:
Isso nos dá
Passo 4
Beleza, agora vamos montar a integral:
Nas novas variáveis
Temos, então
Show? Lembrando que temos que levar para a integral o módulo do Jacobiano.
Aplicando os intervalos que encontramos:
Passo 5
Agora é só resolver isso aí