Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 4612345678910111213141516171819202122232425262728293031323334353637383940414243444547484950515253545556575859606162636465666768697071727374757677787980818283

Enunciado

Calcule a integral

∬ D x 2 + y 2 3   d A ,

onde D é a região limitada pelas hipérboles x 2 - y 2 = 1 ,   x 2 - y 2 = 4 ,   x y = - 1   e   x y = 1 ,   no semiplano direito.

Sugerão: Use a transformação u = x 2 - y 2 ,   v = x y e calcule o Jacobiano usando o fato de que J u ,   v = 1 J x , y , onde J x , y = ∂ u , v ∂ x , y . E mostre que x 2 + y 2 2 = u 2 + 4 v 2

Passo 1

Para calcularmos essa integral, vamos começar ouvindo a sugestão do enunciado, certo?

u = x 2 - y 2

v = x y

Substituindo esses valores nos limites para encontramos onde u e v estão variando ficmaos com:

x 2 - y 2 = 1  

x 2 - y 2 = 4  

x y = - 1  

x y = 1

Logo temos que :

1 ≤ u ≤ 4

- 1 ≤ v ≤ 1

Passo 2

Calculando o jacobianos fazemos:

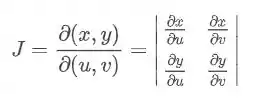
No entanto, observe que não temos x e y em função de u e v, e sim u e em função de x e y. Por essa razão à sugestão do enunciado.

Fazemos então:

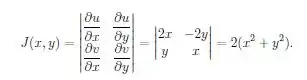
O jacobiando que estamos procurando é a inversa desse, ou seja:

Passo 3

𝑇emos ainda que escrever o jacobiano em função da mudança de parâmetros. Na minha opinião esse é o passo mais chato.

Temos basicamente que relacionar x 2 - y 2   e   x y com x 2 + y 2

Observa isso comigo:

x 2 + y 2 2 = x 2 - y 2 2 + 4 x 2 y 2

Opa, isso já salva nossa vida:

x 2 + y 2 2 = u 2 + 4 v 2

x 2 + y 2 = u 2 + 4 v 2

Passo 4

Montando e resolvendo nossa integral ficamos com:

∬ D x 2 + y 2 3 d A =

1 2 ∫ 1 4 ∫ - 1 1 u 2 + 4 v 2 u 2 + 4 v 2   1 u 2 + 4 v 2   d A =

1 2 ∫ 1 4 ∫ - 1 1 u 2 + 4 v 2 d A =

1 2 ∫ 1 4 u 2 v + 4 v 3 3 | 1 - 1 d u =

1 2 ∫ 1 4 2 u 2 + 8 3 d u =

1 2 2 u 3 3 + 8 u 3 | 4 1 =

1 2 160 3 - 10 3 =

Resposta

25

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .