Mudança de variáveis
Seja . Calcular o valor da integral
Passo 1
Essa expressão parece complicada tanto para integrar em quanto em , pois o termo dentro da raiz quadrada não é muito simples. Vamos, então, procurar uma substituição que facilite essa integração. Faremos:
e
Assim, o radicando passa a ser simplesmente .
Passo 2
Agora vamos calcular o Jacobiano dessa transformação.
Escrevendo as equações de e de em função das novas variáveis e , temos o sistema:
.
Temos, então>
Passo 3
Agora vamos calcular os novos intervalos. Como a região de integração fica mais complexa nas variáveis e , vamos fazer o gráfico no plano :
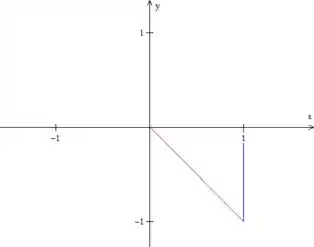
Assim, fica mais fácil ver que e , pois a reta vermelha é . Precisamos, agora, “traduzir” esses limites para as novas variáveis, substituindo os valores que atribuímos a e a :
Passo 4
Agora vamos montar a nova integral em termos de e :
Passo 5
Integraremos, então, em relação a :
Passo 6
Integraremos, então, em relação a :