Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 5312345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152545556575859606162636465666768697071727374757677787980818283

Enunciado

UFMG, Sem Campus, Cálculo 3, P1 - 2021.2, Questão 1.

A integral iterada ∫ 0 ln ⁡ 3 ∫ 2 x 2 ln ⁡ 3 e y 2 d y d x vale

a) ln ⁡ 3

b) 8

c) 1

d) 81

e) 20

Passo 1

Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nesse problema, temos que calcular a integral ∫ 0 ln ⁡ 3 ∫ 2 x 2 ln ⁡ 3 e y 2 d y d x .

Bora começar? 👀

Se tentássemos calcular essa integral na forma como ela está, seria muito difícil então o que temos que fazer é inverter a ordem de integração.

Porém não basta simplesmente inverter as integrais, temos que adaptar os limites de integração

Portanto a primeira coisa a se fazer é esboçar a região de integração para reescrever os limites de integração.

Sacou? Bora lá! 😁

Passo 2

Antes, tínhamos que y = 2 x e y = 2 ln ⁡ 3 eram os limites em y e x = 0 e x = ln ⁡ 3 eram os limites em x .

Esboçando essas curvas, vamos obter

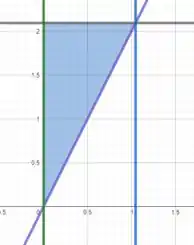
Agora o que temos que fazer é definir os limites em x através de duas funções e em y através de duas constantes.

Vemos que a região em x varia de x = 0 até x = y 2 e em y varia de y = 0 até y = 2 ln ⁡ 3

Assim, nossa nova integral é dada por

∫ 0 2 ln ⁡ 3 ∫ 0 y 2 e y 2 d x d y

Começando integrando com relação a x , temos

∫ 0 y 2 e y 2 d x = x e y 2 x = 0 y 2

∫ 0 y 2 e y 2 d x = y 2 e y 2

Tranquilo até aqui? 😉

Passo 3

Integrando y 2 e y 2 pelo método da substituição fazendo u = x 2 e d u = 2 x d x

∫ 0 2 ln ⁡ 3 y 2 e y 2 d y = e y 2 4 y = 0 2 ln ⁡ 3

∫ 0 2 ln ⁡ 3 y 2 e y 2 d y = e 2 ln ⁡ 3 2 4 - e 0 2 4

∫ 0 2 ln ⁡ 3 y 2 e y 2 d y = e 4 ln ⁡ 3 4 - 1 4

Simplificando...

∫ 0 2 ln ⁡ 3 y 2 e y 2 d y = 3 4 4 - 1 4

∫ 0 2 ln ⁡ 3 ∫ 0 y 2 e y 2 d x d y = 20

E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta

e) 20

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .