Calcule a integral, efetuando a mudança de variáveis apropriada
a) , onde é a região do primeiro quadrante limitada pela elipse .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular a integral dupla sobre a do primeiro quadrante limitada pela elipse . Essa região define nossa região de integração, aí em amarelo:
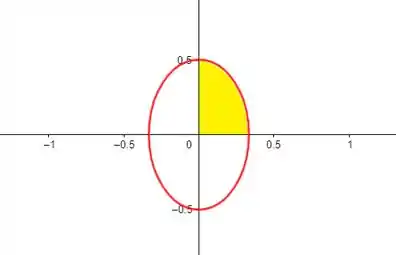
Nós vamos usar as equações de transformação:
Assim, teremos:
Além disso, vamos usar a definição:
Onde é o Jacobiano da transformação, que é dado da seguinte forma:
Então, vamos calcular as derivadas parciais de e , tirar esse determinante e substituir na integral junto com os intervalos de integração.
Vamos lá!
Passo 2
Vamos começar calculando as derivadas do nosso Jacobiano.
Temos que é a derivada de em função de :
E é a derivada de em função de :
Temos que é a derivada de em função de :
E por ultimo é a derivada de em função de :
Passo 3
Pronto, agora é só substituir e calcular:
Passo 4
Show! Agora a gente pode reescrever a integral assim:
onde é a parte do disco no quarto quadrante.
Então, essa integral vai se tornar mais fácil de calcular se passarmos para coordenadas polares, fazendo e :
Integrando em relação a e , respectivamente:
E aplicando os limites de integração:
Valeu, galera! Até a próxima! 😉