Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 3212345678910111213141516171819202122232425262728293031333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283

Enunciado

Calcule a integral dupla

∬ D   x - y e x + y x - y d x d y ,

Onde D é o trapezoide com vértices 1 ,   0 , 2 ,   0 , 0 ,   - 2 , 0 ,   - 1 .

Dica: Faça uma mudança de variáveis para simplificar o integrando.

Passo 1

Bem, a primeira coisa que devemos fazer em um exercício desses é fazer um esboço da região D .

Como o problema nos informou os pontos, basta coloca-los no gráfico

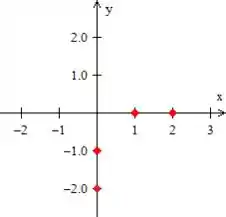
e liga-los com retas formando assim o trapezoide pedido !

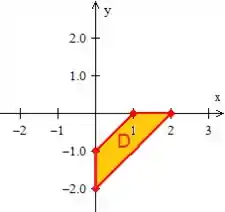
Prontinho! Região definida!

Passo 2

Mas espera! Uma coisa muito importante aqui é definir as equações dessas quatro retas que descobrimos:

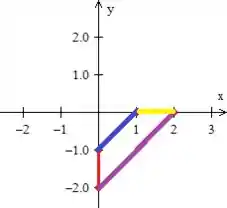
  • A retinha vermelha é fácil, pois ela é paralela a y e tem coordenada x sendo 0, logo sua equação é justamente x = 0 .
  • A reta amarela é muito semelhante a vermelha, mas dessa vez y = 0 .
  • Bem, quanto a reta rosa, ela é um pouquinho mais chata de se determinar. Como que a gente vai fazer isso? Bem, a gente vai se lembrar da equação geral da reta y = A x + B e para determinar o A e o B , basta jogar dois pontos conhecidos da reta nessa equação, veja só:

O primeiro ponto é que esta na reta rosa é ( 0 ,   - 2 ) , então (jogando em y = A x + B

- 2 = A ∙ 0 + B       ⇒         B = - 2

O segundo ponto é ( 2 ,   0 )

0 = A ∙ 2 - 2

A = 1

Logo a equação da retinha rosa que queríamos é y = x - 2

  • Fazendo o mesmo para encontrar a equação da reta azul, ou seja, jogando dois pontos conhecidos da reta azul 0 ,   - 1 e 1 ,   0 encontramos:

- 1 = A ∙ 0 + B         ⇒           B = - 1

                          0 = A ∙ 1 - 1       ⇒         A = 1                          

Portanto a equação da azul é y = x - 1

Passo 3

Pois então, como o próprio problema nos sugeriu, devemos fazer uma mudança de variáveis para simplificar essa coisa horrorosa que devemos integrar: ∬ D   x - y e x + y x - y d x d y . Note que aqui fica mais simples se fizermos:

x - y = u

x + y = v

Percebeu?

Bem, toda vez que fazemos uma mudança, devemos buscar as variações dessas. E como a gente pode fazer isso aqui?

Usando as equações das retas que determinamos!

Veja só, utilizando as equações da reta rosa e da azul:

y = x - 2

y = x - 1

Notamos que elas são bem parecidas, e mais, se a gente passar esse y pro lado de lá nos dois casos

0 = x - y - 2

0 = x - y - 1

Em seguida jogar esses números pro primeiro lado, vamos obter

2 = x - y

1 = x - y

Como fizemos x - y = u , ganhamos que u varia dentro de

1 ≤ u ≤ 2

Passo 4

Para determinar agora a variação de v , vamos substituir as equações das outras duas ( x = 0 e y = 0 ) retas que sobraram nas novas equações das variáveis, dessa forma aqui:

x = 0             ⇒ S u b s t i t u i n d o   e m         x - y = u x + y = v

0 - y = u 0 + y = v  

Concluímos aí que v = - u

Agora substituindo y = 0 (a equação da ultima reta amarela)

y = 0             ⇒ S u b s t i t u i n d o   e m         x - y = u x + y = v

x - 0 = u x + 0 = v

Ou seja v = u

Dessas duas coisas que determinamos, podemos concluir que v

- u ≤ v ≤ u

Passo 5

Bem, a gente não pode esquecer de modo algum que quando fazemos uma mudança, temos que encontrar o Jacobiano J dessa mudança, ok?

Mas aqui, como fizemos uma mudança das novas variáveis em função das velhas

u = x - y

v = x + y

A gente pode simplesmente encontrar o Jacobiano inverso J - 1 e depois relacionar com o Jacobiano que a gente quer, já que J = 1 J - 1

Se lembra da fórmula do Jacobiano inverso?

J - 1 = ∂ u ∂ x ∂ u ∂ y ∂ v ∂ x ∂ v ∂ y

Logo

J - 1 = 1 - 1 1 1

Calculando o determinante

J - 1 = 1 - 1 1 1 = 1 - - 1 = 2

Portanto o Jacobiano será

J = 1 J - 1 = 1 2

Passo 6

Retornando agora para integral dupla

∬ D   x - y e x + y x - y d x d y

e trocando as variáveis pelas novas, não esquecendo de multiplicar pelo Jacobiano

∬ D u v   u   e v u ∙ J   d A

Esse D u v aí apenas tá indicando as variações de u e v . Por falar nisso, substituindo os limites desses caras

∬ D u v   u   e v u ∙ J   d A = ∫ 1 2 ∫ - u u u   e v u ∙ 1 2   d v d u

Bem, agora basta resolver essa integral dupla aí! Bora?:D

Passo 7

Jogando esse 1 2 pra fora da integral dupla e calculando a integral de dentro

1 2 ∫ 1 2 ∫ - u u u   e v u   d v d u =

Lembre-se que se a gente vai integrar em relação à v primeiro, podemos passar esse u pra fora da integral de dentro

1 2 ∫ 1 2 u ∫ - u u e v u   d v d u

Pra resolver essa integral em relação à v , vamos fazer uma mudança de variável

v u = a           ⇒               d a = 1 u d v

Portanto d v = u d a

Não se esqueça de trocar os limites também:

v = - u           a = - u u = - 1

v = u           a = u u = 1

Substituindo tudo...

1 2 ∫ 1 2 u ∫ - u u e v u   d v d u = 1 2 ∫ 1 2 u ∫ - 1 1 e a   u   d a d u

Novamente tirando esse u

1 2 ∫ 1 2 u 2 ∫ - 1 1 e a   d a d u =

Integral da exponencial é a própria exponencial...

1 2 ∫ 1 2 u 2 e a - 1 1 d u =

Substituindo os limites em e a

1 2 ∫ 1 2 u 2 e - e - 1 d u =

Passando essa constante de dentro dos parênteses pra fora

e - e - 1 2 ∫ 1 2 u 2 d u =

E integrando em u

e - e - 1 2 u 3 3 1 2 =

Substituindo os limites

e - e - 1 2 2 3 3 - 1 3 3 =

7 e - e - 1 6

Resposta

∬ D   x - y e x + y x - y d x d y = 7 e - e - 1 6

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .