Stewart, James. Cálculo, volume 2, ed 7ª – Capítulo 15 – Seção 10 – Questão 25
Calcule a integral, efetuando uma mudança de variáveis apropriada.
Onde é a região trapezoidal com vértices:
Passo 1
E aí, amigão desse outro lado da tela? Pronto para mais um exercício de mudança de variável? Nesse exercício vamos propor uma transformação e calcular a integral.
Olhando para nossa função dentro da integral:
Nós vemos duas expressões:
Então vamos começar usando a seguinte as transformação baseadas nos elementos de dentro da função:
Como queremos determinar quem será o , vamos subtrair uma equação da outra:
Chegamos então ao resultado:
Podemos encontrar o valor de usando a soma das duas equações:
Então:
Passo 2
Para continuarmos a usar a mudança de variáveis, precisamos calcular o jacobiano da transformação, que nada mais é do que descobrir o determinante da matriz abaixo:
As derivada parciais são mais tranquilas de resolver, temos que considerar apenas a variável que estamos interessadas na hora de derivar, por exemplo:
Queremos derivar a expressão em relação a , então tudo que não for pode ser considerado constante:
Logo, fazendo isso para todas as outras parcelas, chegamos em:
Para encontrar o determinante, você deve fazer o produto da diagonal principal:
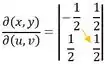
E subtrair do produto da diagonal secundária:
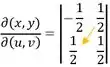
Logo nosso determinante é:
Passo 3
Observe que é a imagem da região trapezoidal com vértices Isso nos leva a escrever a integral da seguinte maneira: