Use a mudança de coordenadas
para calcular a integral
Onde é o polígono de vértices e .
Passo 1
Cara, ele deu os vértices de um polígono em , que é nosso domínio . E deu a mudança de coordenadas
A primeira coisa que a gente precisa fazer é entender como esse domínio fica quando passa por essa transformação. Qual é a cara dele no plano ? Sabendo isso, a gente consegue limitar as variáveis e , para termos nossos extremos de integração, beleza?
Uma forma de fazer isso, é achar a imagem dos pontos que temos em no plano . E como a gente pode fazer isso? Cara, a gente precisa das expressões para e em função de . Vamos achar elas através das expressões que a gente tem.
A gente monta um sisteminha com as expressões da mudança de coordenadas. E queremos achar em função de e em função de .
Se a gente multiplicar a de baixo por e somar as duas equações que ficarem:
Agora voltando para o primeiro sisteminha, a gente pode multiplicar a equação de cima por :
Prontinho, achamos as expressões que a gente queria:
Passo 2
Agora é achar como é a cara de quando passa por essa tranformação, e vira um domínio em . Como a gente faz isso? Cara, vamos jogar cada pontinho de que a gente tem nessas expressões. E assim, a gente acha novos ponto em .
- Ponto :
Daí a gente tira o ponto .
- Ponto
Daí a gente tira o ponto .
- Ponto
Daí a gente tira o ponto .
- Ponto
Daí a gente tira o ponto .
Achamos então um novo polígono com vértices em e . Olha como é o desenho dele:
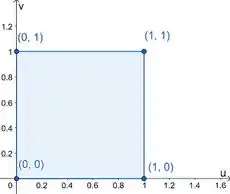
Olha que alegria: nosso domínio ficou retangular nesse plano! Então a gente pode limitar nossas duas variáveis entre constantes, dessa forma:
Passo 3
Mas já que falamos de mudança de variáveis, a gente precisa calcular o jacobiano dessa mudança!
E módulo dele fica
Passo 4
Com os extremos de integração e o jacobiano, a única peça que falta é mudar as variáveis do integrando. A gente vai sair de e ir para .
Nossa integral é
E nosso integrando é
Aí para transformar ele numa função de , é só usarmos nossas expressões para a mudanças de variáveis:
Substituindo no integrando
Prontinho!
Passo 5
Agora vamos montar a nossa integral, a gente multiplica esse integrando por e coloca os extremos de integração:
Passo 6
Agora é calcular essa belezinha
Vamos usar uma propriedade de potência para reescrever esse integrando
Como a gente vai integrar em relação a , podemos tirar esse termo em da integral:
Agora, fazendo uma substituição simples , achamos: