Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 2412345678910111213141516171819202122232526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283

Enunciado

Mudança de variáveis

Calcule, efetuando uma mudança de variáveis conveniente, a integral

∫ ∫ R   cos ⁡ x - y sin ⁡ x + y   d A

Onde R é a região trapezoidal com vértices ( 1,0 ) , ( 2,0 ) , ( 0,2 ) e ( 0,1 ) .

Passo 1

Vamos começar esboçando essa região para entender melhor o problema. Lançando esses pontos em um gráfico, temos isso aqui:

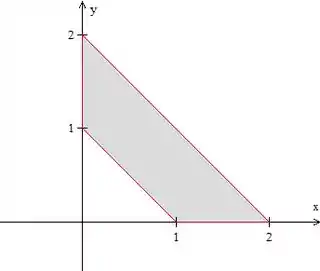
Como o problema disse, um trapézio.

Como podemos ver, nossa região está limitada pelas retas:

x = 0

y = 0

Essas são fáceis de ver, certo? Temos também as retas inclinadas:

y = - x + 1

y = - x + 2

Para achar essas equações, você pode substituir os pontos na equação geral da reta y = a x + b . Ou, pode simplesmente ver pelo gráfico que os coeficientes das retas são a = - 1 , uma vez que elas cortam os eixos x e y no mesmo ponto e estão inclinadas para a esquerda. Como elas cortam o eixo y em + 1 e + 2 , os coeficientes b são esses.

Passo 2

Beleza, precisamos resolver a integral

∫ ∫ R   cos ⁡ x - y sin ⁡ x + y   d A

Onde R é limitada pelas retas:

x = 0

y = 0

y = - x + 1         →           y + x = 1

y = - x + 2           →             y + x = 2

Bem... tem muito " y + x " e " y - x " nessa história aí, né? Tanto na integral como nas retas que limitam a região. Então, fazer uma substituição:

y + x = u

x - y = v

Parece uma boa. Vamos fazer isso. Vamo isolar x e y nessa mudança. Somando as duas equações, temos:

2 x = u + v         →         x = u + v 2

x - y = v           →       y = u + v 2 - v = u - v 2

Passo 3

Agora vamos calcular o Jacobiano disso aí.

Temos

x = u + v 2

y = u - v 2

J = ∂ ( x , y ) ∂ ( u , v )     = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v

∂ x ∂ u = 1 2

∂ x ∂ v = 1 2

∂ y ∂ u = 1 2

∂ y ∂ v = - 1 2

J = 1 2 1 2 1 2 - 1 2 = - 1 4 - 1 4 = - 1 2

Lembre-se de que queremos o módulo do Jacobiano:

J = 1 2

Fazendo a substituição na integral, temos, então:

∫ ∫ R   cos ⁡ x - y sin ⁡ x + y   d A =

= 1 2 ∫ ∫ R *   cos ⁡ v sin ⁡ u   d A =

Passo 4

Agora vamos escrever a nova região de integração. Fazendo a substituição nas retas que limitam R , temos:

y + x = 1         →       u = 1

y + x = 2         →         u = 2

Temos também:

x = 0

x = u + v 2 = 0           →         - v = u

y = 0

y = u - v 2 = 0         →         v = u

Resumindo, as novas retas são as seguintes:

u = 1

u = 2

v = u

v = - u

Graficamente:

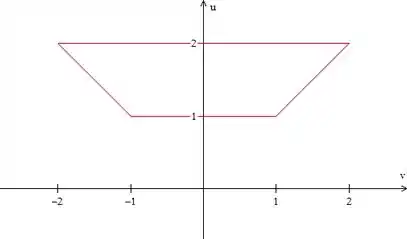
Podemo ver, então, que u varia entre 1 e 2 , logo, 1 ≤ u ≤ 2 e que v varia entre as retas v = u e v = - u , portanto, - u ≤ v ≤ u .

Aplicando isso na nossa integral, temos:

1 2 ∫ 1 2 ∫ - u u cos ⁡ v sin ⁡ u   d v d u

Passo 5

Agora vamos integrar isso aí. Primeiro em relação a v :

= 1 2 ∫ 1 2 sin ⁡ v sin ⁡ u - u u d u =

= 1 2 ∫ 1 2 sin ⁡ u - sin ⁡ - u sin ⁡ u d u =

= 1 2 ∫ 1 2 sin ⁡ u - - sin ⁡ u sin ⁡ u d u =

= 1 2 ∫ 1 2 2 sin ⁡ u sin ⁡ u d u =

= ∫ 1 2 d u =

Agora em relação a u :

= u 1 2 =

= 2 - 1 = 1

Resposta

1

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .