Calcule a integral dupla , onde é a região delimitada pelas curvas dadas pelas equações , , e .
Passo 1
Essa integral, não parece muito simples de se calcular. Analisando o domínio, não conseguimos identificar de primeira que região é essa, para escrevermos como tipo I ou II. Por isso, precisamos fazer substituições.
Repare que os termos e aparecem tanto na integral como nas curvas que limitam a região de integração, isso nos leva a pensar que talvez seja uma boa substituí-los por outra variável. É que faremos, vamos definir:
e
Passo 2
Agora vamos calcular o Jacobiano dessa transformação.
Escrevendo as equações de e de em função das novas variáveis e , temos o sistema:
.
Temos, então>
Você também poderia ter calculado e invertido o resultado
Passo 3
Agora vamos calcular os novos intervalos, substituindo e as equações das curvas do enunciado:
Nos planos , essas expressões definem a seguinte região:
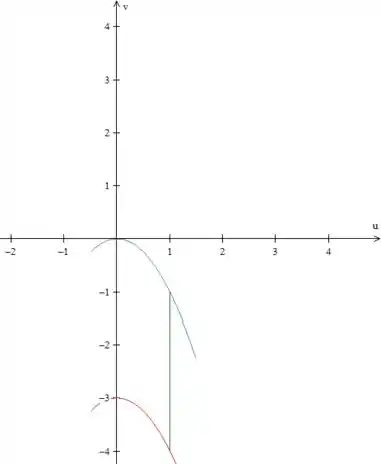
A curva vermelha e a azul são parábolas viradas para baixo.
Passo 4
Vamos, agora, escrever esse domínio como tipo I (em cima e embaixo temos funções e à esquerda e à direita demos números). Como podemos ver, varia de a , portanto:
A variável está entre a curva vermelha e azul , assim temos:
Passo 5
Agora vamos montar a nova integral, substituindo os valores de e :
Passo 6
Integraremos, então, em relação a :
Passo 7
Para terminar a integração, faremos a substituição , temos
Assim, conseguimos “eliminar” esse termo que multiplica os cossenos. Vamos reorganizar aqui nossa integral:
Passando o sinal de menos pra dentro, invertemos a ordem da subtração