Mudança de variáveis
Seja . Calcule
Passo 1
Bom, já deu pra perceber que temos algumas vezes na questão, não é? Vamos fazer a seguinte mudança de variáveis então:
Isso vai simplificar bastante a região de integração.
Passo 2
Como toda e qualquer mudança, precisamos de um Jacobiano:
Passo 3
Agora, vamos fazer um gráfico desse domínio para podermos encontrar o novo domínio.
é esse triângulo:
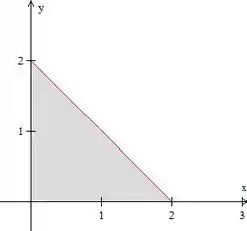
Olhando para essa figura, podemos escrever que:
O que nos dá:
Ou seja
Passo 4
Agora vamos levar tudo o que achamos para a integral e fazer a mudança de variáveis:
Passo 5
Agora vamos resolver isso aí. Vamos começar invertendo essa ordem de integração.
A região
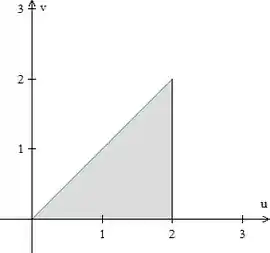
Passa a ser
Resposta
Exercícios de Livros Relacionados
Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .