Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 5912345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758606162636465666768697071727374757677787980818283

Enunciado

Calcule a seguinte integral:

∫ 0 2 ∫ y 2 y + 4 2 y 3 2 x - y e 2 x - y 2 d x d y

Passo 1

Bem, essa integral parece esquisita e difícil de calcular, né?

Então vamos tentar fazer uma mudança de váriavel pra ver se simplifica as coisas. Seria muito bom se uma das variáveis fosse u = 2 x - y , mas vamos entender a região primeiro pra ver se dá pra fazer assim mesmo.

A gente tem uma região do tipo 2 , com 0 ≤ y ≤ 2 e y 2 ≤ x ≤ y + 4 2 :

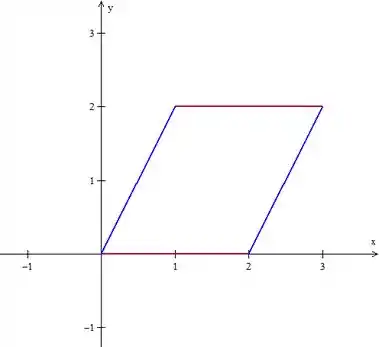
Mas essas retas x = y 2 e x = y + 4 2 são exatamente:

  x = y 2 → 2 x - y = 0

x = y + 4 2 → 2 x - y = 4

Então a transformação u = 2 x - y é sim muito conveniente, a outra pode ser v = y mesmo já que ele aparece na integral e tem seus limites constantes.

Passo 2

Então vamos ficar com:

2 x - y = 0 → u = 0

2 x - y = 4 → u = 4

0 ≤ u ≤ 4

0 ≤ v ≤ 2

E o jacobiano a gente calcula a partir de J * , já que temos as variáveis u e v isoladas, ao invés de x e y :

J * = ∂ ( u , v ) ∂ ( x , y )     = ∂ u ∂ x ∂ u ∂ y ∂ v ∂ x ∂ v ∂ y

∂ u ∂ x = 2           ∂ u ∂ y = - 1

∂ v ∂ x = 0         ∂ v ∂ y = 1

J * = 2 - 1 0 1 = 2

Então, temos:

J = 1 J * → J = 1 2

E nossa integral fica:

∫ 0 2 ∫ y 2 y + 4 2 y 3 2 x - y e 2 x - y 2 d x d y = ∫ 0 2 ∫ 0 4 v 3 u e u 2 1 2   d u d v

Passo 3

Calculando, chegamos em:

1 2 ∫ 0 2 v 3 d v ∙ ∫ 0 4 u e u 2 d u

⇒ 1 2 ∙ v 4 4 │ 0 2 ∙ ∫ 0 4 u e u 2 d u = 2 ∫ 0 4 u e u 2 d u

Que a gente resolve fazendo a substituição:

t = u 2 → d t = 2 u   d u

Então:

∫ e u 2 2 u   d u = ∫ e t d t

⇒ e t = e u 2

Aplicando os limites de integração, ficamos com:

e u 2 │ 0 4 = e 4 2 - e 0 2

⇒ e 16 - 1

Resposta

e 16 - 1

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .