USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 8c
Calcule as seguintes integrais, invertendo a ordem de integração:
c)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente inverter a ordem de integração e calcular a integral dupla dada. Pra inverter a ordem de integração, a gente precisa inverter os limites de integração e a melhor forma de visualizar isso é observando o gráfico da região dada pelos limites. Nesse caso, temos:
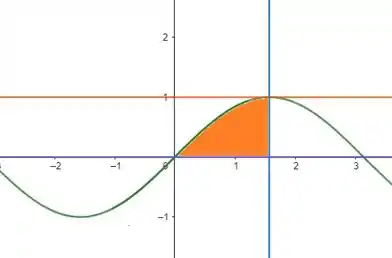
A gente vai tentar escrever nossa integral com , então temos que olhar primeiro como varia e verificar, em seguida, como varia no gráfico. Assim, vamos calcular nossa nova integral.
Vamos lá!
Passo 2
Olhando nosso gráfico, a gente percebe que varia de até e que vai de até a curva ou . Assim, temos:
Então, montando nossa integral, temos:
Assim, integrando primeiro em relação a :
Aplicando os limites de integração em :
Passo 3
Agora para integrar em relação a , vamos primeiro simplificar um pouco nossa expressão, usando a identidade trigonométrica :
Agora vamos chamar , pra facilitar nossa vida na hora de integrar. Assim, temos:
Como a gente definiu , nossa derivada é na verdade:
Então, substituindo na integral, vai ficar:
Integrando agora, temos:
Voltando pra nossa variável , vamos ter:
Aplicando os limites de integração em :
Como e , vamos obter:
Valeu, galera! Até a próxima! 😉