Calcule a integral dupla
Onde . Sugestão: use mudança de variáveis.
Passo 1
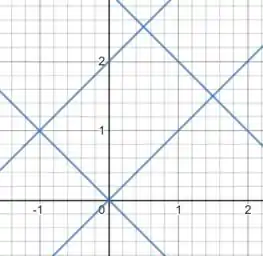
Então pessoal, vamos começar tentando desenhar essa região .
O primeiro passo é dar uma olhada nessas condições que o enunciado deu:
Isso vai dar duas retas decrescentes, uma passando pela origem e a outra passando pelo ponto .
Isso vai dar duas retas crescentes, uma passando pela origem e a outra passando pelo ponto .
Beleza, todas essas condições envolvem retas. Se a gente desenhar essas retas no plano cartesiano, dá pra ver qual é a região em que estamos integrando:
Passo 2
Tá, dá pra ver que aquela região é simplesmente um retângulo um pouco inclinado.
Vamos pensar em uma mudança de variáveis que facilite o trabalho de encontrar os limites de integração. Bom, a região é definida assim:
Uma boa tentativa é essa mudança de variáveis aqui:
Nesse caso os limites de integração ficariam bem tranquilos:
Então beleza, vamos escrever a integral inteira com essas variáveis.
Primeiro precisamos escrever e em função de e usando esse sistema aqui:
Somando as duas equações:
E substituindo isso na primeira equação:
Então:
Ok, vamos em frente.
Passo 3
Vamos reescrever a função com as nossas novas variáveis:
Ao invés de sair substituindo, vamos tentar reorganizar isso antes. Se a gente rescrever assim, por exemplo:
Beleza, aqui já fica fácil de mudar algumas coisas:
O primeiro termo em parênteses é o produto notável e o segundo é uma diferença de quadrados:
Então, escrevendo em função de e :
Ou seja, nossa integral fica assim:
Passo 4
Antes de integrar, precisamos dar um jeito de substituir o . Vamos tentar fazer isso usando essa fórmula:
Onde é o jacobiano, que tem como fórmula o determinante de uma matriz:
Tá, pra resolver isso vamos primeiro calcular cada uma dessas derivadas parciais. Por sorte elas são bem tranquilas de calcular:
Então a matriz do Jacobiano fica assim:
E agora é só calcular o determinante:
Então:
Substituindo isso na integral:
Agora é só colocar aqueles limites de integração que mencionamos lá em cima:
Passo 5
E o próximo passo é resolver a integral:
Primeiro vamos integrar em relação a :
Nesse passo aí usamos o fato de que e
E voltando à integral:
Beleza, esse é o resultado da integral.
Resposta
A integral vale .