Calcule a integral dupla
Onde é a região, no primeiro quadrante, limitada pelas curvas , , , e .
Passo 1
Vamos esboçar no plano cartesiano essas 4 curvas que delimitam a nossa região. Repare que e representam circunferências de centro na origem, sendo a primeira de raio 1 e a segunda, raio 3.
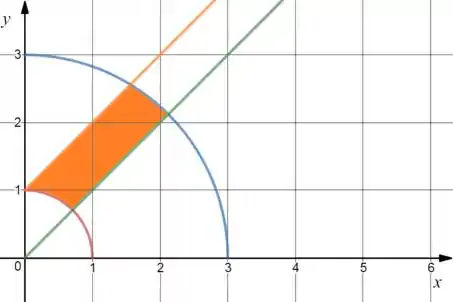
Passo 2
Repare bem que a região que vamos calcular a integral não é muito amigável de se definir em termos de e , logo, vamos tentar realizar uma mudança de variável. Belaza, mas qual é a mudança de variável que nos ajudaria?
Bem... vejamos as equações das nossas curvas:
Repare que essas curvas são bem parecidas umas com as outras nos possibilitando fazer a seguinte mudança:
Onde os limites de e ficam sendo
Passo 3
Vamos agora encontrar o Jacobiano da nossa mudança de coordenadas.
Como temos as nossas novas variáveis em termos das nossas antigas, ficará mais fácil calcular o jacobiano inverso
Porém, não nos interessa muito o Jacobiano inverso e sim o módulo do jacobiano. Não tem problema, pois a gente sabe que
Porém a gente sabe que a região R está no primeiro quadrante, logo
Passo 4
Se a gente está fazendo uma mudança de coordenadas, não podemos deixar de mudar as variáveis da função, correto? Então vem comigo
A nossa função de integração é dada por
Podemos separar essa subtração no seguinte produto notável
Repare que os dois primeiros termos desse produto final temos uma substituição direta. Mas o que vamos fazer para substituir esse ?
Nós não vamos substituir e sabe o porquê?
Por que quando fazemos uma mudança de variável, não estamos interessados na função pura, e sim no produto dela pelo jacobiano
Viu! Aquele termo desaparece! :) Agora podemos substituir direto
Passo 5
Só nos resta montar a integral e atacar! Bora lá? :)
Resolvendo a integral de dentro e depois substituindo na de fora obteremos: