Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 2134567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283

Enunciado

Considere a aplicação g definida por:

x = u + v

y = v - u 2

Utilizando g , calcule ∬ D   x - y + 1 4 - 1 2 d x d y , onde D é a imagem no plano x y da região Q no plano u v limitada pelas retas u = 0 , v = 0 e u + v = 2 .

Passo 1

Como o enunciado já disse as substituições que devemos fazer, precisamos agora calcular o Jacobiano dessa transformação. Já temos x e y escritos em função de u e v , não é?

x = u + v

y = v - u 2

Temos J = ∂ ( x , y ) ∂ ( u , v )     = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v

∂ x ∂ u = 1

∂ x ∂ v = 1

∂ y ∂ u = - 2 u

∂ y ∂ v = 1

J = 1 1 - 2 u 1 = 1 1 - 1 - 2 u = 1 + 2 u

Passo 2

Sabemos que, no plano x y , a região de integração é dada por D , como está na integral do problema. Passando as coordenadas para u e v , a região passa a ser Q , como o próprio enunciado diz. Agora vamos fazer as substituições na integral:

∬ Q     u + v - v - u 2 + 1 4 - 1 2 ⋅ ( 1 + 2 u ) d u d v =

= ∬ Q   u + u 2 + 1 4 - 1 2 ⋅ ( 1 + 2 u ) d u d v =

= ∬ Q   u + 1 2 2 - 1 2 ⋅ ( 1 + 2 u ) d u d v =

= ∬ Q   u + 1 2 - 1 ⋅ ( 1 + 2 u ) d u d v =

= ∬ Q   2 u + 1 2 - 1 ⋅ ( 1 + 2 u ) d u d v =

= ∬ Q   2 2 u + 1 ⋅ 1 + 2 u d u d v =

∬ Q   2   d u d v

Passo 3

Agora precisamos descrever essa região Q , limitada por u = 0 , v = 0 e u + v = 2 no plano u v . Vamos fazer um esboço.

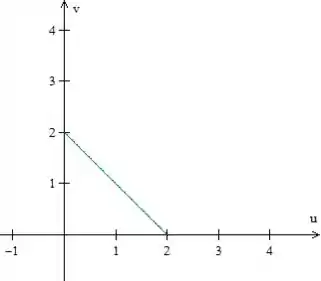
Podemos descrevê-la como região do tipo I, com 0 ≤ u ≤ 2 e 0 ≤ v ≤ 2 - u . A integral iterada será:

∫ 0 2 ∫ 0 2 - u 2   d v d u =

Passo 4

Integrando em relação a v , temos:

= ∫ 0 2 2 v v = 0 v = 2 - u d u =

= ∫ 0 2 2 2 - u d u =

= ∫ 0 2 4 - 2 u   d u =

Passo 5

Integrando, agora, em relação a u :

= 4 u - u 2 0 2 =

= 8 - 4 =

Resposta

4

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .