USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 15b
Calcule usando mudança de coordenadas:
b) , onde é a região do primeiro quadrante limitada pelas retas e .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular uma integral meio estranha em um domínio limitado por retas. Isso é a dica para a gente usar uma mudança de variáveis linear!
Como assim? Mudança de variáveis linear é quando a gente aplica uma mudança com express��es assim no nosso domínio:
Onde são constantes. A ideia é que essa mudança vai deixar nosso integrando bonito e vai transformar nosso domínio mais fácil de integrar. Vamos usar isso então! Mas que expressões podemos testar para e ? Vamos ver isso pelo integrando:
Seria melhor se fosse , né? Então, podemos fazer:
Agora é ver se ela funciona bem no domínio. Vamos lá!
Passo 2
Para a mudança e , somando as expressões, teremos:
Substraindo as expressões, teremos:
Portanto:
Passo 3
Pronto, já escolhemos nossa substituição, agora vamos calcular seu Jacobiano:
Temos:
Assim:
Em módulo:
Passo 4
Agora vamos calcular os novos intervalos. Antes tínhamos , e os eixos coordenados e limitando nossa região de integração. Vamos substituir as novas variáveis nessas expressões:
No plano , essas expressões definem a seguinte região:
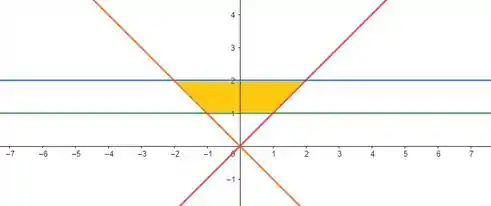
Então, como podemos ver, temos os intervalos:
Passo 5
Então, montando nossa integral, vai ficar:
Vamos usar a substituição simples , assim:
Além disso, quando , temos e quando , temos . Então, vai ficar:
Calculando agora em relação a e aplicando os intervalos:
Valeu, galera! Até a próxima! 😉