Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 8112345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808283

Enunciado

UNICAMP, Sem Campus, Cálculo 2, Atividades Profº Plínio Santini - Atividade 2, Questão 6

Calcule a integral

∫ ∫ D e x 2 - y 2 d A

Onde D =   { ( x ,   y )   ∈   R 2 |   y   +   1   ≤   x   ≤   y   +   2 ,   y 2   −   1   ≤   x 2   ≤   y 2   +   1 } .

Sugestão: utilize a mudança de variável u   =   x   +   y   e   v   =   x   −   y .

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Cálc 2. Nosso objetivo é calcular a integral

∫ ∫ D e x 2 - y 2 d A

Onde D =   { ( x ,   y )   ∈   R 2 |   y   +   1   ≤   x   ≤   y   +   2 ,   y 2   −   1   ≤   x 2   ≤   y 2   +   1 } .

E temos a dica utilize a mudança de variável u   =   x   +   y   e   v   =   x   −   y

Passo 2

Vamos usar a nossa dica, e reescrever nosso domínio. Como

u   =   x   +   y   e   v   =   x   −   y

Então,

D = {   y   +   1   ≤   x   ≤   y   +   2 ,   y 2   −   1   ≤   x 2   ≤   y 2   +   1 }

Logo

D * =   1   ≤   v   ≤   2 ,   y 2   −   1   ≤   v u   ≤   1 }

Esse domínio é bem mais simples. Vamos desenhar:

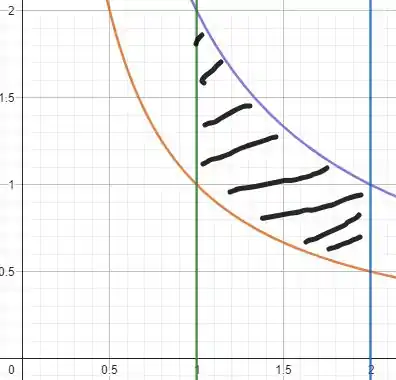
Passo 3

Agora podemos resolver nossa integral. Como sabemos nosso novo domínio, e como

u   =   x   +   y   e   v   =   x   −   y

Fazendo o determinante da matriz jacobiana obtemos:

| J | = 1 / 2

D * =   1   ≤   v   ≤   2 ,   y 2   −   1   ≤   v u   ≤   1 }

Logo, nossa integral fica:

∫ ∫ D e x 2 - y 2 d A = 1 2 ∫ ∫ D * e x y d A  

= 1 2 ∫ 1 2 ∫ - 1 / v 1 / v e u v d u d v

Integrando, temos:

= 1 2 ∫ 1 2 1 v e u v | u = 1 / v u = - 1 / v d v

= 1 2 ∫ 1 2 e v - 1 e v d v

Integrando em v

= 1 2 e l n ( v ) - l n ( v ) e | v = 2 v = 1

= 1 2 ( e l n ( 2 ) - e - 1 l n ( 2 ) )

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

= 1 2 ( e l n ( 2 ) - e - 1 l n ( 2 ) )

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .