Stewart, James. Cálculo, volume 2, ed 7ª – Capítulo 15 – Seção 10 – Questão 26
Calcule a integral, efetuando uma mudança de variáveis apropriada.
, onde é a região do primeiro quadrante limitada pela elipse
Passo 1
Fala aí, pessoal, mais um exercício de mudança de variável e
Nesse exercício vamos propor uma transformação e calcular a integral.
Olhando para nossa função dentro da integral:
Como temos dois elementos elevados ao quadrado, vamos usar a seguinte transformação:
Assim, teremos:
Você viu esse truque chegando, certo?
Passo 2
Para continuar a integral mudando suas variáveis, precisamos calcular o jacobiano da transformação, ou seja, descobrir o determinante da matriz abaixo:
As derivada parciais são mais tranquilas de resolver, temos que considerar apenas a variável que estamos interessadas na hora de derivar, por exemplo:
Queremos derivar a expressão em relação a , então tudo que não for pode ser considerado constante:
Faremos o mesmo para as outras derivadas:
Substituindo em nossa matriz chegamos a:
Para encontrar o determinante, você deve fazer o produto da diagonal principal:
E subtrair o produto da diagonal secundária:
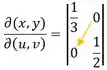
Logo nosso determinante é:
Passo 3
Show! Agora a gente pode reescrever a integral assim:
onde é a parte do disco no quarto quadrante.
Então, essa integral vai se tornar mais fácil de calcular se passarmos para coordenadas polares:
Nas coordenadas polares, podemos encontrar através da expressão:
Que o raio deve estar entre:
Enquanto como estamos falando no enunciado que estamos no primeiro quadrante, o ângulo está dentro do intervalo:
Também devemos fazer as mudanças:
Então nossa integral se torna:
Podemos separa as duas integrais em relação a e em relação a :
O nosso resultado final é:
Arassamos!!!! Vai firme para a próxima!