Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 6612345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656768697071727374757677787980818283

Enunciado

UNICAMP – Sem campus – Cálculo 2 – P2 – 6º Manhã- 4

Usando uma mudança de variáveis, calcule a integral

∫ ∫ y - 2 x 3 y + 2 x   d A

Onde D é o paralelogramo de vértices: (1, 2), (2, 4), (5, 2) e (4, 0).

Passo 1

Fala turminha, tudo em cima? Bora lá resolver essa questão. Primeiro, vamos desenhar o nosso domínio definido pelo paralelogramo.

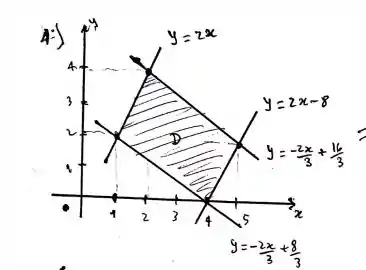
Com isso, nosso domínio fica delimitado por 4 equações que vai ser bem complexo da gente trabalhar depois, daí, fazemos a mudança de variável que a questão nos propôs. De forma que nosso paralelogramo agora seja:

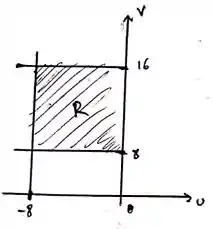
Que vai ser muito mais fácil da gente trabalhar.

Passo 2

Agora precisamos fazer o mais importante quando mudamos as coordenadas, que é o jacobiano. Você sabe como ele é feito? Calculamos da seguinte forma: Primeiro isolamos as variáveis:

u = y - 2 x

v = 3 y + 2 x

Agora, isolando x e y :

x = - 3 u + v 8

E

y = u + v 4

Calculando agora o Jacobiano, temos:

J u , v = d x d u d x d v d y d u d y d v = - 3 8 1 8 1 4 1 4  

Calculando o determinante:

J = - 1 8

J = 1 8

Passo 3

Agora montamos a integral com o nosso novo formato de u e v :

∫ ∫ y - 2 x 3 y + 2 x   d A = ∫ ∫ u v   1 8 d u   d v

Resolvendo a integral:

∫ ∫ u v   1 8 d u   d v = ∫ 8 16   ∫ - 8 0 u v   d u   d v

= 1 8 ⋅ ∫ 8 16 d v v ∫ - 8 0 u   d u

= 1 8 ⋅ ln ⁡ 16 8 0 + 64 2

= 32 8 ln ⁡ 2

= 4 ln ⁡ 2

Resposta

∫ ∫ y - 2 x 3 y + 2 x   d A = 4 ln ⁡ 2

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .