Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 6512345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364666768697071727374757677787980818283

Enunciado

Seja D ⊂ R 2 o dominio do primeiro quadrante limitado pelas curvas planas cujas equações implícitas são: y = 0 ,   x = 1 - y 2 ,   x = 4 1 - y 2 .

a) Esboce a região D

b) Descreva a região do primeiro quadrante do plano u v que corresponde a D mediante a mudança de variáveis: T u ,   v = v 1 - u 2   ,   u ,   u ,   v ≥ 0 .

c) Calcule o Jacobiano de T

d) Calcule a integral dupla ∬ D e y x   d x d y        

Passo 1

a) Desenhando as funções temos o seguinte:

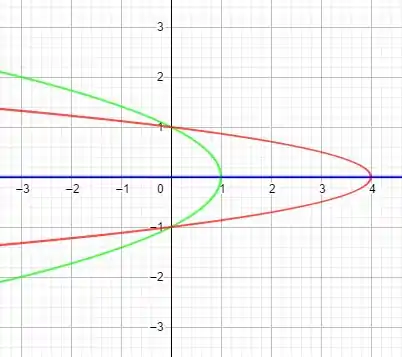
Temos a reta y = 0 , e as parábolas   x = 1 - y 2   e x = 4 1 - y 2

Para encontrar onde as parábolas se encontram igualamos as duas funções

1 - y 2 = 4 1 - y 2

Essa igualdade só é válida se y = ± 1 . Temos então que os pontos onde elas se interceptam são

( 1,0 ) ( - 1,0 )

Como ele nos pede a região do primeiro quadrante e limitada por essas funções

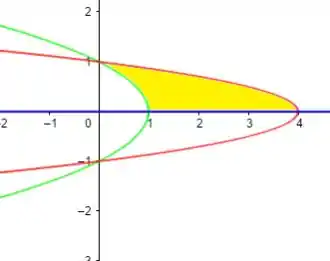
Passo 2

b) A mudança de variável T u ,   v = v 1 - u 2   ,   u ,   u ,   v ≥ 0 nos dá que

x =   v 1 - u 2   y = u

Utilizando essa mudança de variáveis nas equações

y = 0 :

u = 0

x = 1 - y 2 :

v 1 - u 2   = 1 - u 2

v 1 - u 2   - ( 1 - u 2 ) = 0

1 - u 2   ( v - 1 ) = 0

v = 1 ou   u = ± 1

x = 4 1 - y 2 :

  v 1 - u 2   = 4 1 - u 2

1 - u 2   ( v - 4 ) = 0

v = 4 ou u = ± 1

Como na questão ele diz que é pra considerar o primeiro quadrante então nossos limites serão:

0 ≤ u ≤ 1

1 ≤ v ≤ 4

Essa região é um retângulo uma vez que u   e v   variam entre valores constantes

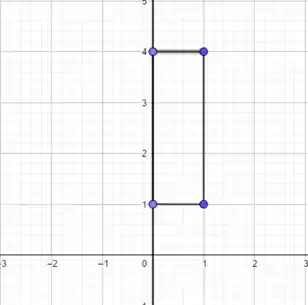
Passo 3

c) O Jacobiano pode ser calculado assim:

J = ∂ ( x , y ) ∂ ( u , v ) = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v

Calculando as derivadas parciais

Lembrando que x =   v 1 - u 2   e y = u

∂ x ∂ u = - 2 u v

∂ x ∂ v = ( 1 - u 2 )

∂ y ∂ u = 1

∂ y ∂ v = 0

J = - 2 u v 1 - u 2 1 0 = - 2 u v . 0 - 1 1 - u 2 = u 2 - 1

Passo 4

d) Para calcularmos essa integral podemos utilizar a nossa mudança de variável que fizmos anteriormente

x =   v 1 - u 2   y = u

A integral fica assim

∬ D e y x   d x d y = ∫ 1 4 ∫ 0 1 e u v 1 - u 2   J d u d v

Onde | J |   é o módulo do Jacobiano que sempre precisamos calcular quando fazemos uma mudança de variável.

Parece que complicou mas quando substituirmos o Jacobiano que já calculamos e vale u 2 - 1   nossa vida fica mais fácil

∫ 1 4 ∫ 0 1 e u v 1 - u 2   ( u 2 - 1 ) d u d v = - ∫ 1 4 ∫ 0 1 e u v d u d v

Integrando com relação a u

= - ∫ 1 4 1 v e u ​ 0 1 d v

= - ∫ 1 4 1 v ( e - 1 ) d v

= 1 - e ∫ 1 4 1 v d v

Integrando com relação a v

= 1 - e ln ⁡ v ​ 1 4

= ( 1 - e ) ( l n 4 - 0 )

= l n 4 ( 1 - e )

Resposta

Letra a)

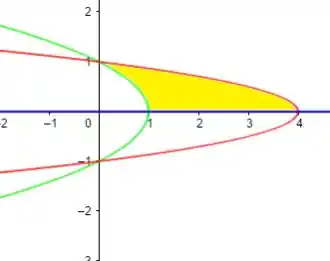
Letra b)

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .