Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 6212345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061636465666768697071727374757677787980818283

Enunciado

Questão 2: Use a mudança de coordenadas x = 2 u + v , y = u + 2 v , para calcular a integral dupla da função x + 3 y na região triangular com vértices 0 ,   0 , 2 ,   1 e 1 ,   2 .

Passo 1

Bem, um exercício com muitas informações, mas calma! Vamos começar definindo o que a gente quer:

Queremos uma integral dupla dessa forma aqui:

∬ D   x + 3 y   d A

Onde D é o triangulo do problema com os vértices 0 ,   0 , 2 ,   1 e 1 ,   2 :

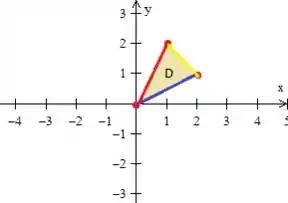
Passo 2

Tá, se vamos realizar uma mudança, a gente necessita das equações dessas retas que delimita o triângulo, certo?

Toda equação de reta é dado por y = a x + b onde temos que encontrar o a e o b , então para encontrar cada uma dessas retas, basta substituir 2 pontos dela, veja só...

  • Para a reta azul...

    • 1 º   p o n t o     0 ,   0     ⇒         y = a x + b       →               0 = 0 a + b →             b = 0

    2 º   p o n t o   2 ,   1     ⇒         y = a x + b       →               1 = 2 a →             a = 1 2              

    Então a reta azul é y = 1 2 x

  • Para a reta vermelha...

    • 1 º   p o n t o     0 ,   0     ⇒         y = a x + b       →               0 = 0 a + b →             b = 0

    2 º   p o n t o   1 ,   2     ⇒         y = a x + b       →               2 = a →             a = 2                      

    Então a reta azul é y = 2 x

  • Finalmente para a reta amarela...

    • 1 º   p o n t o     2 ,   1     ⇒         y = a x + b       →               1 = 2 a + b

              2 º   p o n t o   1 ,   2     ⇒         y = a x + b       →               2 = a + b            

    Resolvendo esse sisteminha isolando o a na de baixo e substituindo na de cima...

    1 = 2 a + b     →         1 = 2 2 - b + b         →

    1 = 4 - b     →       b = 3

    E a = 2 - b = - 1

    Logo a reta amarela é y = - x + 3 .

    Passo 3

    Com essas equações de retas em mãos, a gente pode substituir a mudança de variável pedida no problema: x = 2 u + v e y = u + 2 v .

  • Na reta azul...

    • y = 1 2 x       →           u + 2 v = 1 2 2 u + v         →

    u + 2 v = u + 1 2 v  

    Jogando tudo para um lado só...

    3 2 v = 0             e n t ã o           v = 0

  • Na reta Vermelha...

    • y = 2 x       →           u + 2 v = 2 2 u + v         →

    u + 2 v = 4 u + 2 v

    Jogando tudo para um lado só...

    - 3 u = 0             e n t ã o           u = 0

  • Na amarela...

y = - x + 3           →                 u + 2 v = - 2 u - v + 3       →

3 u = 3 - 3 v       ÷ 3   →

u = 1 - v

Percebe agora porque precisamos das equações das retas que delimita a região? Veja que no plano u v , as três equações que encontramos

v = 0 ,           u = 0             e           u = 1 - v

Forma um triângulo bonitinho...

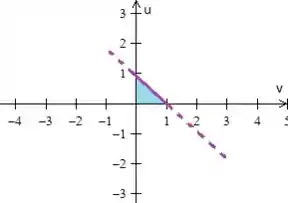
Passo 3

Se vamos calcular uma integral dupla em cima de u e v pela mudança, temos que descrever essa região:

Podemos fazer isso descrevendo como uma região do tipo 1 :

0 ≤ u ≤ 1 - v

0 ≤ v ≤ 1

Passo 4

Em toda e qualquer mudança a gente sempre tem que calcular o Jacobiano que é dado por:

J = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v

Como

x = 2 u + v

y = u + 2 v

Então...

J = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v = 2 1 1 2 =

4 - 1 = 3

Então o módulo do Jacobiano de que vamos precisar...

J = 3

Passo 5

Finalmente podemos retornar a integral dupla que queremos resolver...

∬ D   x + 3 y   d A

Vamos trocar o x e o y ...

x + 3 y = 2 u + v + 3 u + 2 v =

5 u + 7 v

Vamos então jogar esse resultado na integral não se esquecendo de multiplicar pelo módulo de J ...

∬ D   x + 3 y   d A = ∫ 0 1 ∫ 0 1 - v 5 u + 7 v ⋅ J   d u d v =

3 ∫ 0 1 ∫ 0 1 - v 5 u + 7 v   d u d v

Bora calcular essa integral aí?

Passo 6

Calculando a integral de dentro...

3 ∫ 0 1 ∫ 0 1 - v 5 u + 7 v   d u d v = 3 ∫ 0 1 ∫ 0 1 - v 5 u + 7 v   d u d v =

3 ∫ 0 1 5 u 2 2 + 7 v u 0 1 - v d v =

E substituindo os limites lembrando de substituir em u , pois foi nele quem integramos primeiro...

3 ∫ 0 1 5 1 - v 2 2 + 7 v 1 - v d v =

3 ∫ 0 1 5 - 10 v + 5 v 2 2 + 7 v - 7 v 2 d v = 3 ∫ 0 1 5 2 + 2 v - 9 2 v 2 d v =

3 5 2 v + v 2 - 3 2 v 3 0 1 =

3 5 2 + 1 - 3 2 =

Finalmente obtemos...

6

Resposta

6

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .