Seja a região do primeiro quadrante limitada por , , e e seja a mudança de variáveis onde
a) Esboce a região e a região tal que .
b) Usando a mudança de variáveis calcular a integral
Passo 1
a) Cara, esboçar essa região , é esboçar as curvas , , e no primeiro quadrante. E destacar a região que está sendo limitada por todas essas curvas ao mesmo tempo.
Vamos começar por , isso é uma reta que tem angulação de em relação ao eixo , e passa pela origem. Já a é também uma reta que passa pela origem, mas angulação dela é maior.
Colocando essas duas no mesmo plano:
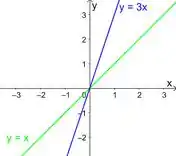
Agora vamos olhar para as outras curvas. Olha essa aqui . A gente pode escrever ela como
E isso é um tipo de hipébole (eles esperam que a gente saiba a cara dela, tá?) E a outra que sobrou: , pode ficar assim
Essa vai ser muito parecida com a hipérbole de cima, mas como o numerador dela é maior, vai ser maior para essa aí. Então ela fica mais acima em relação a anterior.
Aí colocando elas no mesmo plano que as retas e marcando a região (limitada por todas essas curvas), que está no primeiro quadrante, a gente fica com
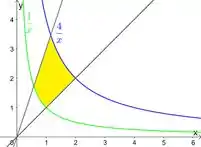
Passo 2
Para esboçar , a gente precisa aplicar nossa mudança :
Nas informações que a gente tem sobre , as curvas: , , e
Percebe que como , podemos reescrever
Agora se a gente reescrever nossas retas assim:
Aí como , temos
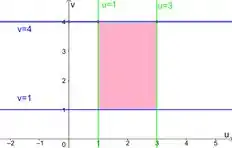
Temos então que é a região entre as retas e . Esboçamos ele no plano assim:
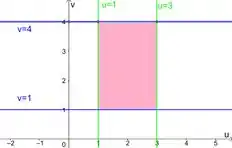
Passo 3
b) Queremos calcular
Mas usando a mudança de variáveis que ele deu. Então já vamos descrever o domínio de integração olhando para , que é a cara de nas variáveis novas e .
Vamos usar essa nova região para ser o domínio da nossa integral. Agora a gente precisa achar nossos extremos de integração.
Repara que no eixo , nossa região é limitada por e . Aí podemos escrever:
Já no eixo , nossa região está entre e . Aí a gente pode dizer que:
Prontinho! Temos nossos extremos!
Passo 4
A gente não pode esquecer do nosso Jacobiano , já que temos uma mudança de variáveis. Como a gente tem e :
Podemos calcular ele pela relação:
Mas a gente precisa do módulo dele. Como estamos no quadrante, a gente sabe que
Então
Passo 5
Agora a gente monta nossa integral nova. Como o nosso jacobiano está em , vamos começar multiplicando o integrando antigo por ele
Esse é o nosso novo integrando, mas a gente precisa colocar ele em função de e . Vamos usar nossas transformações de novo, vendo se a gente acha uma expressão em para :
Esse vai ser nosso integrando final, aí agora a gente só precisa colocar nossos extremos de integração:
Passo 6
Agora é calcular essa belezura:
Como para , o é uma constante:
Resposta
a) 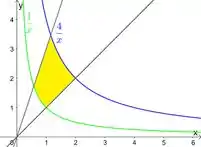
b)