Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 6712345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656668697071727374757677787980818283

Enunciado

UNICAMP – Sem campus – Cálculo 2 – P2 – 5º tarde - 4

Usando uma mudança de variáveis, calcule a integral

∫ ∫ D   y - x 3 1 + x + y d A

Onde D é o triangulo de vértices ( 0,0 ) (1,0) e ( 0,1 ) .

Passo 1

Fala turminha, tudo em cima? Bora lá resolver essa questão. Primeiro, vamos atrás de desenhar o nosso triângulo pra gente ter uma visão gráfica da coisa:

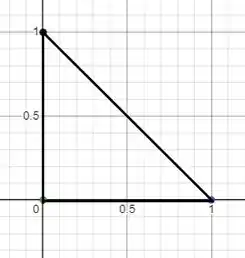
Aqui precisamos integrar a nossa função ao longo do domínio da função, que é justamente esse triângulo que acabamos de desenhar. Aqui, como dica da questão, vamos fazer uma mudança de variáveis. Chamaremos então:

u = y - x

v = 1 + y + x

Logo,

y = 1 2 u + v - 1

x = 1 2 v - 1 - u

Passo 2

Agora, vamos transformar esse domínio triangular em um domínio limitado por duas funções, o que diminui a complexidade dela. Agora vamos remontar a integral. Mas, falta uma coisa: os novos limites de integração. Montando o segundo triângulo (agora depois de transformar as variáveis), temos:

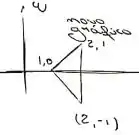
Esse novo gráfico. Nele, os limites de integração vão ser calculados como,

Para d v :

v = 1 + x + y

Primeiro limite do ponto ( 0,0 ) até o ponto ( 1,0 ) :

v = 1 + x + y

v = 1 + 0 + 0 = 1

v = 1 + 0 + 1 = 2

Para d u

u = x - 1

Primeiro limite do ponto ( 2 , - 1 ) até ( 2,1 ) :

v = 0 → 1

E por fim, calculando a integral:

∫ 1 2 d v ∫ 0 1 u 1 3 v d u

∫ 1 2 d v ∫ 0 1 u 1 3 v d u

Integrando primeiro em u :

∫ 0 1 u 1 3 v d u = 3 4   v

Aplicando isso para d v :

∫ 1 2 3 4   v d v = 3 4 ln ⁡ ( 2 )

Resposta

∫ ∫ D   y - x 3 1 + x + y d A = 3 4 ln ⁡ ( 2 )

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .